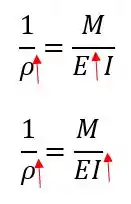
Linha elástica – Conceito
Produzido por Pablo RicardoTeoria
Fala aí, pessoal!!! Vamos hoje vocês vão aprender o que é a linha elástica obaaa!!!
O conceito de linha elástica é muito simples ela é basicamente o diagrama de deflexão de um componente, normalmente uma viga. Só pra lembrar que deflexão é o quanto a nossa viga vai entortar sob efeito de uma carga.
Vamos ver um exemplo prático, imagina que uma viga reta, bi apoiada, é submetida a uma força pontual. Como representado abaixo:
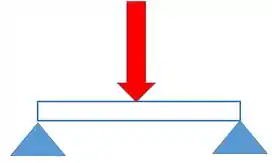
Por causa dessa força a viga vai se deformar da seguinte forma:
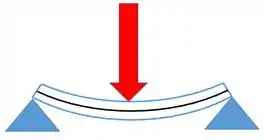
A viga é representada em azul enquanto a linha elástica está em preto. A linha elástica mostra como é a deformação (deflexão) da viga.
Show de bola! Tranquilo né?
A gente consegue chegar nesse resultado que é um esboço de maneira meio lógica, sem fazer contas, seguindo apenas o nosso “instinto engenheirístico”. Mais para a frente nós vamos aprender a calcular essa linha de fato, com vários númerozinhos rs
Mas por agora vamos nos concentrar no esboço da linha elástica e para isso é importante que saibamos as condições de contorno!
Condições de contorno
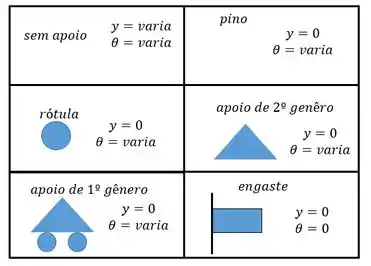
Uma viga sempre vai estar apoiada em alguma coisa não né mesmo? Ela pode estar engastada, apoiada num apoio de primeiro gênero, de segundo gênero, num pino, numa rótula... Enfim, a viga pode estar apoiada de diversas maneiras.

Nessa figura temos diversas vigas em balanço (engastada de um lado e livre do outro) apoiando a “laje em balanço”. Você não vai fazer uma coisa dessas depois que se formar né? kkk.
Tá mas e aí, qual vai ser a diferença de quando uma viga é engastada para quando ela é apoiada? A diferença vai estar em como a viga vai reagir, e ela pode reagir de duas formas:
- Subir ou descer, variação em
- Mudar de angulação, variação em .
Olha lá o exemplo do começo da aula, a gente vai perceber que nos apoios a viga não sobe nem desce, permanece estática. Entretanto, há uma variação no ângulo.
Vamos ver como fica uma laje em balanço, ops... viga em balanço.
Antes da carga:

Depois da carga:

Perceba como o lado engastado não mudou nem de altura nem de angulação. Já o lado livre mudou ambos.
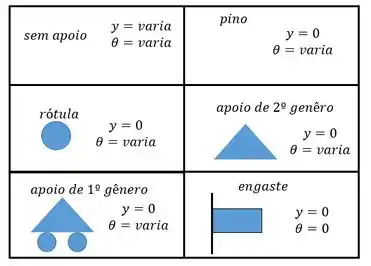
Agora acho que vai ficar um pouco mais fácil de entender a tabela:
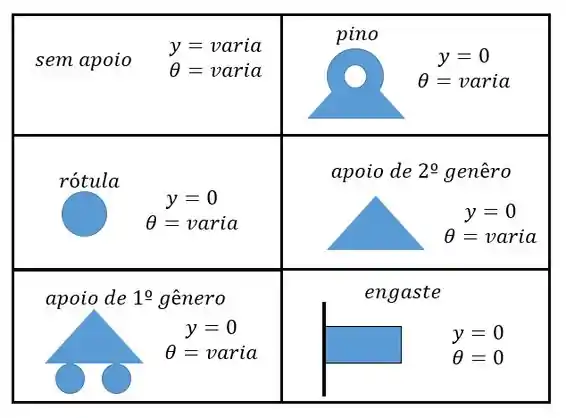
Portanto essas vão ser as nossas condições de contorno!
Flecha e declividade
Muitos problemas vão pedir para calcularmos a flecha ou a declividade em dado ponto. Quando o problema fala em flecha estamos falando da deflexão da viga, ou seja, o valor de .
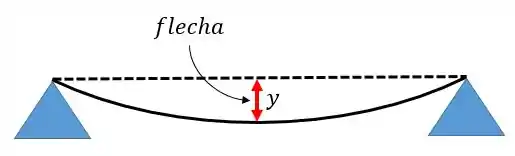
Neste exemplo a linha pontilhada representa a linha elástica antes de carregamento e a linha contínua representa a linha elástica com o carregamento.
Além da flecha vamos ter também a declividade que é, nada mais nada menos, do que o ângulo.
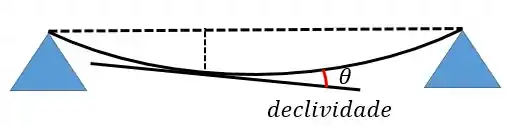
Raio de curvatura
Pessoal, sempre que alguma coisa faz uma curva é possível definir um raio de curvatura para tal curva. O raio de curvatura das vigas vai depender da geometria, do material e da carga.
A geometria é dada pelo momento de inércia , o material pelo coeficiente de elasticidade e a carga pelo momento fletor . Assim, podemos definir o raio de curvatura como:
Aí aqui cabe uma observação! Quando o momento fletor é positivo o raio de curvatura também é positivo e isso representa uma concavidade para cima. Quando o momento fletor é negativo teremos um raio de curvatura “negativo”, que na verdade não é negativo nada, só representa uma concavidade para baixo. (Galera, isso é igual às equações de segundo grau).
Achou que essa aula ia terminar e não ia ter um cálculo né??

Para finalizar a gente ainda pode associar a equação acima à equação da tensão normal. Lembrando que essa equação é dada por:
Aqui representa a distância do ponto que estamos calculando à linha neutra.
Associando as duas vamos ter:
Daí podemos achar a tensão diretamente do raio de curvatura, do coeficiente de elasticidade e da distância do ponto à linha neutra.
Com isso fechamos a nossa aulinha! Partiu para alguns exercícios?
Condições de contorno
Flecha e declividade
Raio de curvatura
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Faça um esboço para a configuração da linha elástica para a viga e carregamento abaixo:
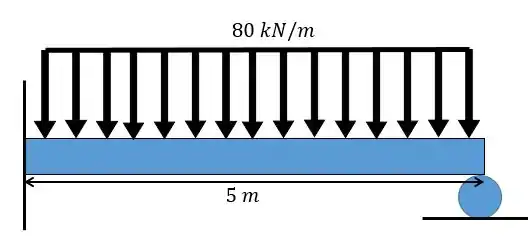
Passo 1
Fala ai, pessoal!! Para fazer o esboço da linha elástica a gente só precisa saber de como os apoios reagem (são as condições de contorno) e de uma ideia do momento fletor na barra.
Precisamos basicamente de duas coisas então: as condições dos apoios e o momento fletor (ao menos uma ideia dele, já que não podemos calculá-lo de fato).
Passo 2
Vamos olhar as condições de contorno. Para as condições de contorno sempre vamos analisar duas coisas: o ângulo e a posição. Neste caso temos um rolete (a bolinha) e um engaste cada um reagirá conforme o esqueminha abaixo:
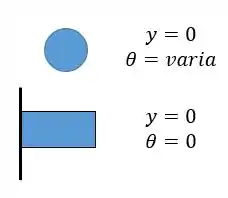
Galera, nos exercícios anteriores a gente fez umas contas para achar o momento fletor mas reparem que, tirando os pontos de apoio nas extremidades, as forças apontam todas para baixo. Logo, a deflexão da barra será para baixo também.
Passo 3
Como o problema pede apenas um esboço então não precisamos ficar calculando o valor exato, basta uma forma aproximada.
Portanto podemos responder apenas com as condições de contorno e o carregamento, não precisamos do momento fletor.
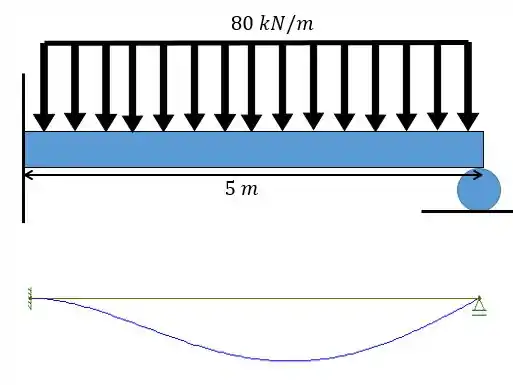
Reparem que a linha elástica começa com uma angulação nula (por causa do engaste), e então começa a descer logo depois, chegando num ponto de máxima deflexão e retorna para o rolete de apoio.
É possível perceber que essa linha elástica possui duas concavidades, uma para baixa logo no começo da viga e a outra para cima no resto da viga. Apesar dessa questão não mencionar nada sobre esse fato é legal notar que nesse ponto de inflexão da viga (onde ocorre a mudança de concavidade) o momento fletor é nulo.
Podemos verificar isso lembrando que quando a concavidade é para baixo o momento fletor é positivo e quando a concavidade é para cima o momento fletor é negativo. Um esqueminha pode deixar mais claro:
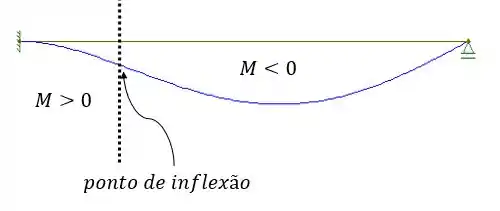
Resposta
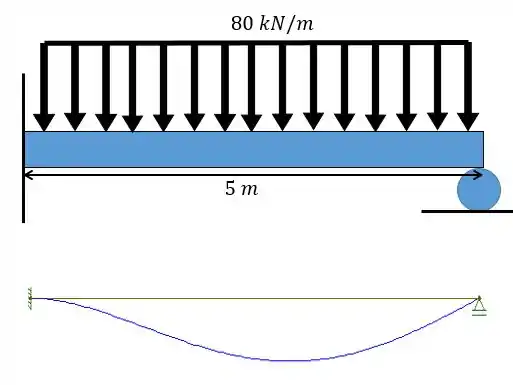
Exercício Resolvido #2
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 440. Problema 12.36 (Adaptada)
Desenhe o esboço da linha elástica da viga abaixo:
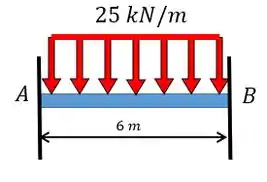
Passo 1
Fala aí, pessoal!! Vamos resolver mais questão introdutória sobre linha elástica que é bem importante para a gente começar a entender esse conceito. A gente precisa principalmente lembrar da nossa tabelinha:
Essa questão pede apenas o esboço da linha elástica, ou seja, não precisamos ficar calculando aqui momento fletor, força cortantes etc e tal. Nesse tipo de exercício vamos focar no que vai acontecer à estrutura de forma mais qualitativa. Resumindo: como você acha que vai ficar a deformação da nossa viga?
Passo 2
A primeira coisa que vamos perceber é que o carregamento empurra a viga para baixo, correto? Além disso é crucial entender o que acontece nos apoios, que nesse caso são engastes. No caso de engastes vamos ter tanto deflexão quanto angulação iguais a zero, portanto nosso esboço vai ser algo da forma:

Aqui o mais importante é ver que nos engastes a angulação é nula!
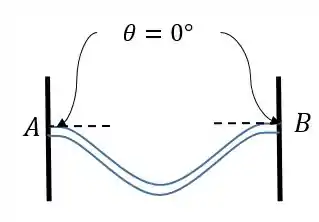
Legal né? Ficou até parecendo uma carinha esquisita =P
Resposta

Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 431. Problema 12.1
Uma tira de aço L2 com 3 mm de espessura e 50 mm de largura é curvada até formar um arco circular de 15m de raio. Determine a tensão de flexão máxima da tira.
Passo 1
Fala aí, pessoal! Antes de mais nada vamos fazer um desenho desse problema para ficar mais fácil de entender:
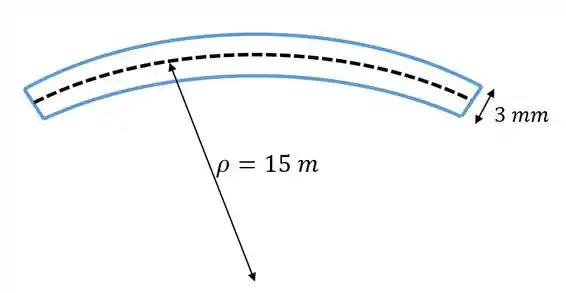
Perceba que ocorre uma flexão e por causa disso existe uma tensão de flexão associada e é isso que o problema nos pede!
Passo 2
A tensão de flexão é dada pela letra e pode ser calculada de diversas formas. A principal delas é:
Onde:
- é o momento fletor.
- a maior distância entre a linha neutra e o ponto que estamos calculando.
- o momento de inércia da seção transversal.
- é o momento fletor.
- é o módulo de elasticidade do material.
- o momento de inércia da seção transversal.
Mas a gente não tem o momento fletor! Temos apenas o raio de curvatura :
Esse dado vai nos ajudar me muito porque podemos achar o momento fletor através do raio de curvatura com a equação:
Onde:
Associando as duas equações vamos ter:
Perceba que temos todas essas grandezas! Agora basta substituir!!
Passo 3
Vamos fazer essa substituição! Observando que, para o aço L2 temos e a distância é a maior distância entre a linha neutra (linha preta pontilhada na figura) e a superfície, dessa forma:
obs: Pegamos o maior valor de porque queremos a máxima tensão de flexão, beleza? Quanto maior o maior o !
Substituindo:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 431. Problema 12.2
A figura de um homem executando um salto em altura com vara permitiu estimar por medição que o raio de curvatura mínimo da vara é 4,5m. Se a vara tiver 40 mm de diâmetro e for feita de plástico reforçado com fibra de vidro, determine a tensão de flexão máxima na vara. .
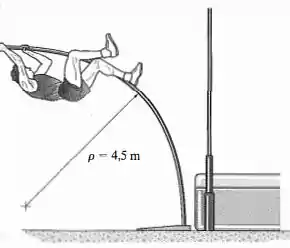
Passo 1
E aí, pessoal? Vamos fazer mais uma?
Nessa questão perceba que ocorre uma flexão e por causa disso existe uma tensão de flexão associada e é isso que o problema nos pede!
Na teoria e no problema anterior a gente viu que a tensão pode ser calculada diretamente se nós já tivermos o raio de curvatura, as dimensões da barra e o coeficiente de elasticidade.
Passo 2
Então é só substituir né! Observando que temos e a distância é a maior distância entre a linha neutra e a superfície, dessa forma:
obs: Pegamos o maior valor de porque queremos a máxima tensão de flexão, beleza? Quanto maior o maior o !
Substituindo:
Resposta
Exercício Resolvido #5
Elaboração própria
Faça um esboço para a configuração da linha elástica para a viga e carregamento abaixo:
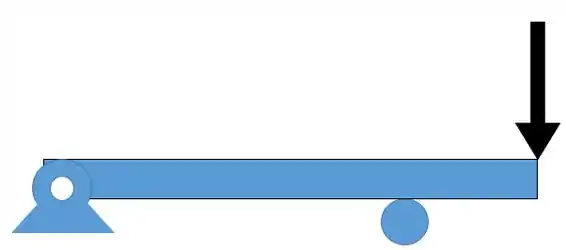
Passo 1
Fala ai, pessoal!! Para fazer o esboço da linha elástica a gente só precisa saber de como os apoios reagem (são as condições de contorno) e de uma ideia do momento fletor na barra.
Precisamos basicamente de duas coisas então: as condições dos apoios e o momento fletor (ao menos uma ideia dele, já que não podemos calculá-lo de fato).
Passo 2
Vamos olhar as condições de contorno. Para as condições de contorno sempre vamos analisar duas coisas: o ângulo e a posição. Neste caso temos um rolete (a bolinha) e um pino ambos reagem da mesma forma, ambos fixam a posição mas estão sujeitos a alterações no ângulo (quanto maior a força maior o ângulo, por exemplo).
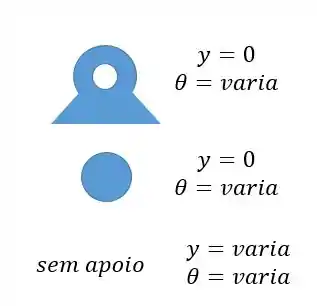
Com isso podemos desenhar a linha elástica:
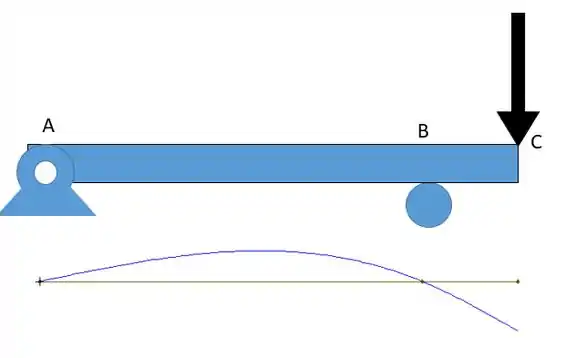
Perceba que a barriga está sempre voltada para baixo, os apoios não possuem alteração de altura mas possuem um ângulo e o ponto que está livre possui tanto uma variação de altura quanto de angulação! É claro que esse ponto se deslocará para baixo devido a força atuante nele!
Pessoal, poderíamos chegar nesse resultado intuitivamente também. Mas quero mostrar como é a resolução padrão. Então vamos dar uma olhada no passo 3 também, que mostra como o momento fletor entra nessa história!
Passo 3
Vamos fazer a análise do momento fletor, para isso vamos fazer um esquema das forças atuantes e para que o sistema se mantenha em equilíbrio vamos ter a seguinte configuração:
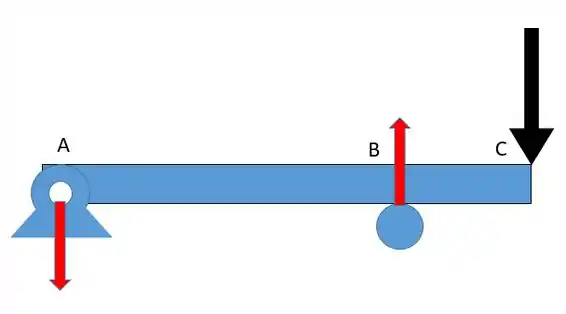
Pessoal, se essa é a configuração de forças (a única possível de forma ao sistema estar em equilíbrio) vamos ter que um momento fletor positivo em todos os pontos da nossa barra. O momento fletor ficaria como algo assim olha:
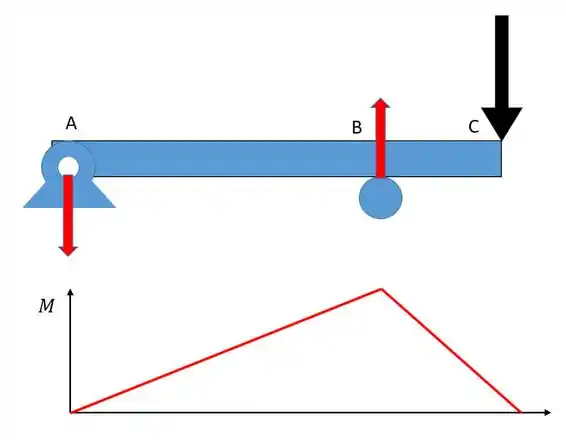
O momento fletor vai ser sempre positivo, além disso será máximo no ponto . Pessoal, se o momento fletor é sempre positivo a “barriguinha” da linha elástica vai apontar sempre para baixo. Assim temos, de fato o desenho que conseguimos no passo 2:

Resposta
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 440. Problema 12.36
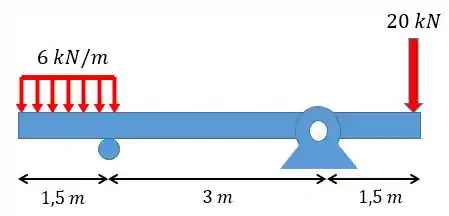
Desenhe o esboço da linha elástica da viga abaixo:
Passo 1
Fala aí, pessoal!! Vamos resolver mais questão introdutória sobre linha elástica que é bem importante para a gente começar a entender esse conceito. A gente precisa principalmente lembrar da nossa tabelinha:
Essa questão pede apenas o esboço da linha elástica, ou seja, não precisamos ficar calculando aqui momento fletor, força cortantes etc e tal. Nesse tipo de exercício vamos focar no que vai acontecer à estrutura de forma mais qualitativa. Resumindo: como você acha que vai ficar a deformação da nossa viga?
Passo 2
Bom, a gente pode imaginar que tanto o carregamento uniforme quanto o pontual vão forçar a nossa viga para baixo. Além disso, temos dois apoios que permitem rotação, logo nesses pontos vai existir uma angulação diferente de zero.
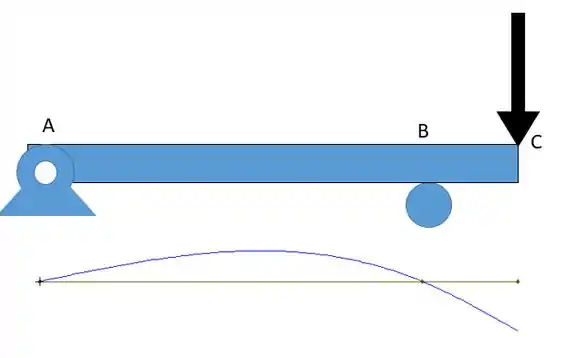
Se nas pontas a viga entorta para baixo então podemos supor também que o meio irá envergar para cima. Como os apoios permitem rotação vamos ter algo do tipo:

Perceba que as angulações nos apoios são diferentes de zero!
Resposta

Exercício Resolvido #7
Elaboração própria
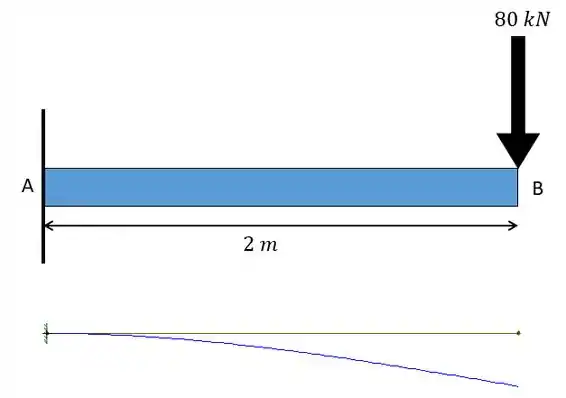
Para a viga de aço (E=200 GPa) e carregamento mostrado a seguir determine o raio de curvatura na metade da viga, faça também um esboço da linha elástica. Dados: Momento de inércia da barra
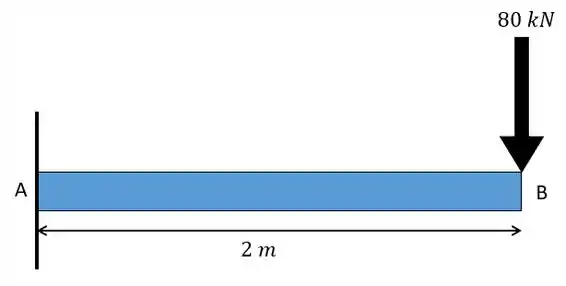
Passo 1
Fala ai, pessoal!! Esse problema começa a introduzir o conceito de linha elástica e pede o esboço dela e o raio de curvatura na metade da viga. Para fazer isso a gente só precisa saber de como os apoios reagem (são as condições de contorno) e achar o momento fletor na barra.
Precisamos basicamente de duas coisas então: as condições dos apoios e o momento.
Passo 2
Vamos olhar as condições de contorno. Para as condições de contorno sempre vamos analisar duas coisas: o ângulo e a posição. Neste caso temos um engaste em e uma extremidade livre em logo as condições são dadas como:
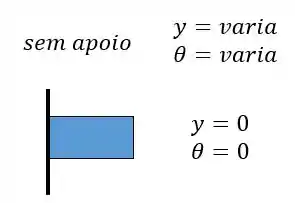
Com isso podemos desenhar a linha elástica:
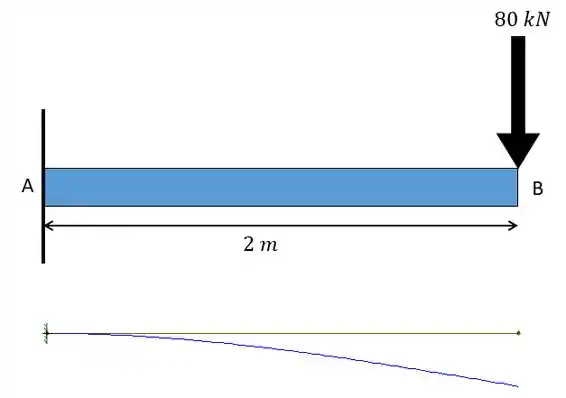
Perceba que a barriga está sempre voltada para baixo, o engaste não possui variação nem de altura nem de angulação enquanto o ponto livre possui variação de ambos.
Então já temos o nosso esboço da linha elástica! Vamos descobrir o raio de curvatura!
Passo 3
Para achar o raio de curvatura temos de achar o momento fletor, para isso vamos fazer um esquema das forças atuantes e para que o sistema se mantenha em equilíbrio vamos ter a seguinte configuração:
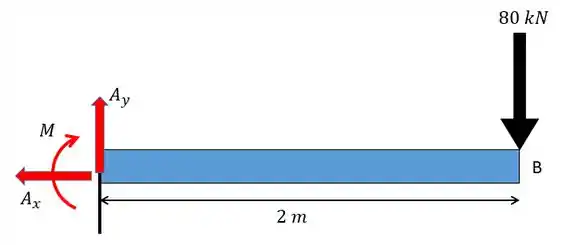
Utilizando as equações de equilíbrio estático vamos obter:
Para :
Para o momento em relação ao ponto e considerando o sentido horário positivo:
Assim podemos achar o momento fletor numa seção qualquer.
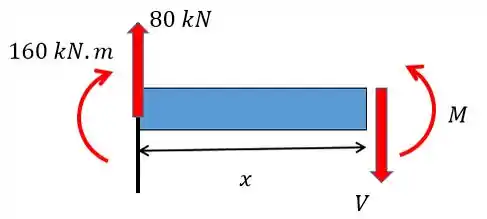
Para achar o momento fletor basta fazer o somatório de momentos em realção ao ponto :
Como a força cortante é igual à força de mas negativa vamos ter:
Assim o diagrama de momento fletor fica da forma:

Bom, na verdade a gente nem precisa fazer o diagrama, mas é legal para perceber que o momento fletor sempre vai ser positivo, isso indica que a linha elástiva sempre vai ter a barriguinha apontada para baixo (ou seja, nosso esboço estava certo! Uhulll)))
Passo 4
Agora vamos achar o raio de curvatura no ponto média da barra. O raio de curvatura pode ser calculado como:
Como queremos o momento fletor em :
E agora é só utilizar os dados da questão:
Resposta
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 432. Problema 12.10 (Adaptada)
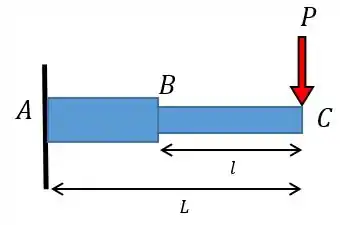
A viga é composta por duas hastes e está sujeita à carga concentrada . Os momentos de inércia são e e o módulo de elasticidade é . Explique o que a diferença entre os momentos de inércia implicam no cálculo do raio de curvatura da nossa viga. Um momento de inércia maior aumenta ou diminui o raio de curvatura? E se fosse o caso de coeficientes de elasticidade diferentes, haveria mudança em ?
Passo 1
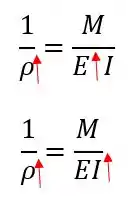
Vamos lá galerinha! Essa questão exige um pouquinho de conhecimento da fórmula do raio de curvatura, que é dada por:
Então o raio de curvatura vai depender do momento fletor , do momento de inércia e do coeficiente de elasticidade . O que a questão pede é saber o que acontece com quando variamos e ?
Passo 2
A primeira coisa que devemos entender é que o momento fletor depende apenas do carregamento, ou seja, nem o momento de inércia e nem o coeficiente de elasticidade interferem no valor de .
Aí olhando para a equação a gente pode ver que tanto quanto são diretamente proporcionais à , portanto quando há um aumento tanto do momento de inércia quanto do coeficiente de elasticidade ocorre um aumento do raio de curvatura:
Galera, é importante perceber que quanto maior for o raio de curvatura então menor será a curvatura da nossa viga, olha só:
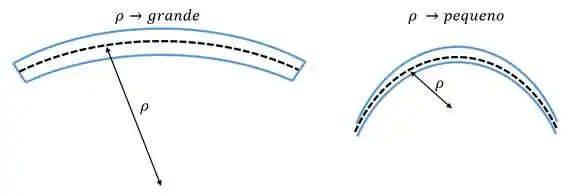
Isso faz sentido correto? Já que um material muito duro ( elavado) vai se deformar menos do que um material macio.
A mesma coisa vale para o momento de inércia. Um blocão de alumínio tem uma curvatura menor do que uma fitinha de alumínio, quando submetidos ao mesmo carregamento.
Resposta
Quanto maior o coeficiente de elastividade e/ou o momento de inércia então maior será o raio de curvatura.