Função de descontinuidade
Teoria
E aí, galerinha da pesada, tranquilão?
Tenho certeza que sim, ainda mais que estão estudando resistência dos materiais HAHAHA.
Mas tenho uma notícia boa para vocês, depois de aprender este conteúdo aqui vocês nunca mais vão resolver uma questão da forma que faziam antes. Acredita nimim!!!
Se liga, vou dar um exemplo. Imagina que a gente quer calcular o momento fletor dessa viga aqui:
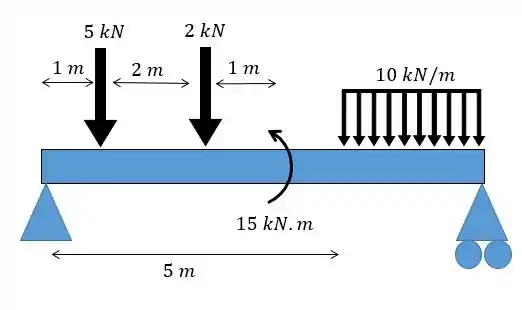
Imaginaa.. Ia ser um saco!!! A gente teria que fazer aí uns 5 cortes para dividir em várias seções e analisar a força cortante e o momento fletor em cada uma!!!
Mas eu vou te ensinar um jeito de fazer isso de uma forma direta, sem ficar cortando em várias seções!! Esse truque mágico enviado por deus são as funções de descontinuidade!
A carinha de uma função de descontinuidade
Uma função de descontinuidade bem simples pode ser escrita como:
Essa simbologia é utilizada para dizer que quando o termo dentre de fica nulo e quando esse termo fica igual ao que realmente tem lá dentro.
Vamos pegar o exemplo anterior pra facilitar um pouco mais. Se a gente tem a seguinte função de descontinuidade ou ela vai ser igual a ou igual a :
Perceba que ela é descontínua, olha que coincidência!!!
Além disso a gente pode colocar expoentes para encontrar outros valores, igual ao exemplo abaixo.
E na prática?
Galera, vamos pegar o nosso exemplo lá do início mas vamos deixar um pouco mais simples. Vamos representar apenas o carregamento distribuído. Peguei leve hein =P
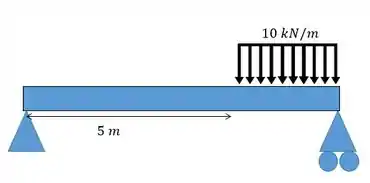
O carregamento distribuído vale:
Vamos entender como esse carregamento funciona, antes de ele não existe e depois de ele existe e é constante e igual a .
Então quando representamos numa função de descontinuidade vai ficar assim
Viu como o fato de estar elevado a zero faz toda a diferença? Por causa deste motivo que o carregamento fica constante, legal né?
Forças e momentos
A gente acabou de ver como um carregamento uniforme pode ser representado. Agora vamos ver para uma força ou momento. Como estes dois elementos atuam pontualmente na viga, vamos chamá-los de funções de singularidade. Mas o princípio é o mesmo.
Imaginem que queremos representar agora o momento de atuante na viga.
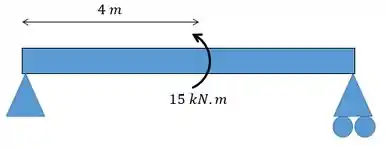
Esse momento atua no ponto e somente nesse ponto, portanto vamos representar como:
Reparem que representamos o momento como uma carga vezes a distância elevado a .
Pessoal, a gente sempre vai colocar a função como um carregamento!!!
Para a força vai ser quase a mesma coisa. Então se a gente for representar as forças da nossa viga vamos ter:
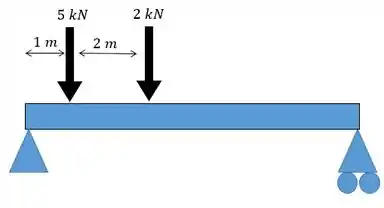
No caso das forças a gente tem que elevar a :
Representando como uma carga
Agora que a gente representou tudo como uma carga vamos ter:
Pessoal, agora que tudo está em podemos somar tudo e obter:
E essa função será válida para toda a viga!! A única coisa que faltou para que a representação fique perfeita é considerar a força do apoio em . Para ficar certinho a gente pode colocar um valor igual a , por exemplo, e agora a representação final da carga será de:
E a valor do apoio final? Não precisa! Porque como ele está lá no final sempre vai ser considerado zero. Pode colocar pra conferir!
Achando a força cortante e o momento fletor
Pessoal, se vocês estiverem sentindo alguma dificuldade fiquem calmos porque quando formos para os exercícios vai cair a ficha de como faz e vocês vão estar fazendo num instante!
Qual a vantagem de utilizar uma equação grandona ao invés de várias pequenas? A vantagem é que é só integrar a função e vamos achar a força cortante depois é só integrar de novo e vamos achar o momento!
Aqui tem que lembrar do sinal hein! Porque a força cortante tem sentido oposto da carga.
Então se a gente quiser achar o momento de uma viga é só colocar tudo como funções de descontinuidade em e integrar duas vezes, sem esquecer do sinal negativo na primeira integral. Por exemplo, se tivermos a função:
A força cortante vai ser dada por:
obs: Repare que quando o expoente é menor ou igual a 0 então a gente só aumenta uma unidade no expoente e deixa o resto todo igualzinho! Quando e expoente é maior do que então fazemos normal, como se fosse um parêntesis.
Considerando o sinal de menos:
Para achar o momento:
Viu como fica rápido?
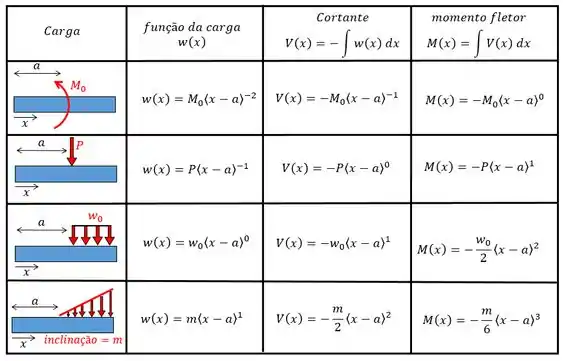
Tabela de cargas, forças cortantes e momentos fletores
Pessoal, vou apresentar vocês uma tabelinha que vai facilitar o entendimento. Essa tabela é um extra, ou seja, com tudo que vocês já viram até aqui já dá para resolver as questões. De qualquer forma vai auxiliar a compreender um pouco melhor essas integrais:
Que tal irmos para uns exercícios pra praticar!?
E na prática?
Forças e momentos
Representando como uma carga
Achando a força cortante e o momento fletor
Tabela de cargas, forças cortantes e momentos fletores
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Utilizando as funções de descontinuidade e de singularidade encontre o momento fletor da seguinte viga:
Passo 1
Bom pessoal vamos aplicar o que vimos na teoria e achar o momento fletor utilizando as equações de descontinuidade. A primeira coisa que temos de fazer é achar todas as forças atuantes na barra, então temos de achar as reações nos apoios.
Feito isso vamos colocar tudo em função de cargas e integrar duas vezes para achar o momento fletor.
Passo 2
Vamos achar as reações nos apoios, para isso a gente vai fazer um desenho das forças:
Como há apenas uma força em vamos ter que:
Fazendo o somatório de forças no eixo :
Agora vamos aplicar o somatório dos momentos em relação ao ponto considerando o sentido anti-horário como positivo:
Voltando ao cálculo:
Substituindo na primeira equação vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
As forças aparecem como:
Repare que a gente tem que considerar a primeira força de apoio mas não a última!
O momento puro aparece como:
Somando os dois termos:
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
Ficou bem grandinho né? haha
Mas é tranquilo, vem comigo!!
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema!
Ajuda muito não é mesmo? Não precisamos fazer um momento de desenhos e cálculos...
Passo 5
Só por curiosidade vamos calcular qual seria o momento fletor em .
Para fazer isso a gente elimina os termos porque e . Daí o que sobra a gente coloca em parêntesis simples, só pra mostrar que eles não vão ser zerados:
Resposta
Exercício Resolvido #2
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 844. Exercício 8 – 2 (Adaptada)
Encontre a equação da linha elástica para a viga abaixo. Considere constante.
Passo 1
Galera essa questão já começa a misturar os tópicos de função de descontinuidade com linha elástica. Então vamos lembrar que o cálculo da linha elástica é feito como:
Vamos achar a linha elástica utilizando esse tipo de função então e calcular a deflexão e a inclinação. Para isso a gente precisa encontrar primeiro o momento fletor e, portanto, as reações. Vamos fazer isso tudo utilizando o conceito de função de descontinuidade que aprendemos =D
Passo 2
Vamos começar achando as reações nos apoios, para isso a gente vai fazer um desenho das forças:
Como há apenas momentos na viga então vamos ter que:
Aplicando o somatório dos momentos vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
Os momentos aparecem da seguinte forma, lembrando que aqui temos de considerar o sentido anti-horário positivo necessariamente:
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
Vamos lá!
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema! Perceba que todos os expoentes são iguais a zero, o que significa que nosso momento fletor varia em degrauzinhos. Isso faz total sentido com o nosso carregamento, que é formado por momentos puros.
Passo 5
Mas o problema pede a equação da linha elástica então nós vamos ter que aplicar a seguinte equação:
Substituindo:
Integrando a primeira vez:
Para descobrir o valor de a gente tem que lembrar que , ou seja, essa nossa equação é da inclinação! Como o ponto está engastado então vamos ter , assim:
Repare aqui que muitos dos termos zeraram, não porque , mas sim por causa da própria natureza da função de descontinuidade.
Agora vamos integrar pela segunda vez:
Agora vamos aplicar o mesmo conceito para achar , como em temos um engaste então a deflexão nesse ponto também é zero, logo:
DICA: Para saber quando uma função de descontinuidade deve ser negligenciada, basta lembrar que o termo dentro dos parêntesis bonitinhos nunca pode ser menor do que zero.
Então finalmente vamos ter a equação da linha elástica:
Resposta
Exercício Resolvido #3
Elaboração própria
Utilizando as funções de descontinuidade e de singularidade encontre o momento fletor da seguinte viga:
Passo 1
Bom pessoal vamos aplicar o que vimos na teoria e achar o momento fletor utilizando as equações de descontinuidade. A primeira coisa que temos de fazer é achar todas as forças atuantes na barra, então temos de achar as reações nos apoios.
Feito isso vamos colocar tudo em função de cargas e integrar duas vezes para achar o momento fletor.
Passo 2
Vamos achar as reações nos apoios, para isso a gente vai fazer um desenho das forças:
Como há apenas uma força em vamos ter que:
Fazendo o somatório de forças no eixo :
A força exercida pela carregamento uniforme é dada por:
Substituindo na equação:
Agora vamos aplicar o somatório dos momentos em relação ao ponto considerando o sentido anti-horário como positivo:
Lembrando que o ponto de atuação da força exercida pelo carregamento uniforme se encontra na metade do carregamento. Fica assim:
Voltando ao cálculo:
Substituindo na primeira equação vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
As forças aparecem como:
obs: A força não aparece porque está na extremidade oposta, não precisamos considerar ela.
A carga uniforme é dada por:
Somando os dois termos:
Passo 4
Agora é só integrar uma vez para achar a força cortante.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
E agora para achar o momento fletor é só integrar novamente.
Pronto! temos a nossa resposta do problema!
Ajuda muito não é mesmo? Não precisamos fazer um momento de desenhos e cálculos...
Passo 5
Galera, sei que já temos o resultado final. Mas imagina que o problema pede para calcularmos o momento fletor no ponto .
Nesse caso como e a gente considera esses valores normalmente (e troca por parêntesis só pra frisar que eles vão ser considerados. E elimina o o termo porque . Vamos ficar com:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 441. Problema 12.42
O eixo suporta as cargas das duas polias mostradas na figura. Determine a equação da linha elática. Os mancais em e exercem somente reações verticais sobre o eixo. constante.
Passo 1
Bom pessoal vamos aplicar o que vimos na teoria e achar o momento fletor utilizando as equações de descontinuidade, para depois aplicarmos a equação da linha elástica:
A primeira coisa que temos de fazer é achar todas as forças atuantes na barra, então temos de achar as reações nos apoios. Feito isso vamos colocar tudo em função de cargas e integrar duas vezes para achar o momento fletor.