Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 15a

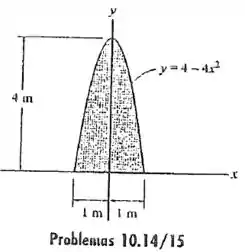
10.15 Determine o momento de inércia da área em relação ao eixo y . Resolva o problema de duas maneiras, usando elementos diferenciais retangulares: (a) com uma espessura de d x e (b) com uma espessura de d y .

Passo 1

a.

A fórmula do momento de inércia em relação ao eixo y é

I y = ∫ A x 2 d A

Nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo y :

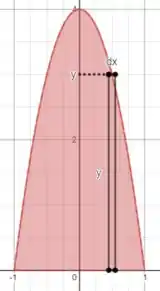
O elemento infinitesimal de área vai ser igual a

d A = y d x

Nós já temos o valor de y :

y = 4 - 4 x 2

Então

d A = 4 - 4 x 2 d x

E os limites de integração vão ir de - 1 até 1 , porque vamos integrar em x .

Passo 2

Então, a fórmula para calcularmos o momento de inercia total, vai ficar:

I y = ∫ - 1 1 x 2 ⋅ 4 - 4 x 2 d x

I y = ∫ - 1 1 4 x 2 - 4 x 4 d x

I y = 4 x 3 3 - 4 x 5 5 - 1 1

I y = 4 1 3 3 - 4 1 5 5 - 4 - 1 3 3 - 4 - 1 5 5

I y = 1 , 067   m 4

Resposta

I y = 1,067   m 4

Ver Outros Exercícios desse livro