Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 23

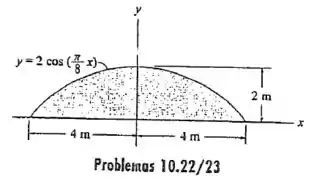
10.23 Determine o momento de inércia da área em relação ao eixo y .

Passo 1

A fórmula do momento de inércia em relação ao eixo y é

I y = ∫ A x 2 d A

Nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo y :

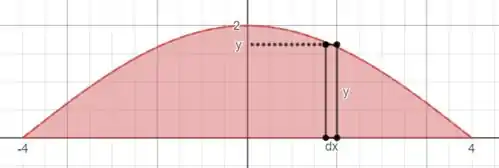
O elemento infinitesimal de área vai ser igual a

d A = y d x

Nós já temos o valor de y , para substituirmos no d A :

y = 2 cos ⁡ π 8 x

Então

d A = 2 cos ⁡ π 8 x d x

E os limites de integraçãoo vão ir de - 4 até 4 , pois vamos integrar em x .

Passo 2

Agora é “só” resolver a integral

I y = ∫ A x 2 d A

I y = ∫ - 4 4 x 2 2 cos ⁡ π 8 x d x

Tirando a constante para fora da integral

I y = 2 ∫ - 4 4 x 2 cos ⁡ π 8 x d x

Essa integral é bemmm chatinha de resolver, vamos precisar usar integração por partes:

∫ u d v = u v - ∫ v d u

Vamos chamar

u = x 2

e

d v = cos ⁡ π 8 x d x

Então

d u = 2 x   d x

e

∫ d v = ∫ cos ⁡ π 8 x d x

v = 8 π ⋅ sen ⁡ π 8 x

A nossa equação vai ficar

∫ u d v = u v - ∫ v d u

∫ - 4 4 x 2 cos ⁡ π 8 x d x = x 2 ⋅ 8 π sin ⁡ π 8 x - 4 4 - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

∫ - 4 4 x 2 cos ⁡ π 8 x d x =

4 2 ⋅ 8 π sin ⁡ π 8 4 - - 4 2 ⋅ 8 π sin ⁡ π 8 - 4 - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

16 ⋅ 8 π 1 - 16 ⋅ 8 π - 1 - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

256 π - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

Precisamos lembrar dessa equação aqui:

∫ - 4 4 x 2 cos ⁡ π 8 x d x = 256 π - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

Porque depois vamos precisar juntar as integrais, que a gente ta calculando, tudo em uma só.

Passo 3

Vamos resolver aquela integral que faltou:

∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

16 π ∫ - 4 4 x sen ⁡ π 8 x d x

Mais uma vez temos que fazer a integração por partes

u = x

e

d v = sen ⁡ π 8 x d x

Então

d u = d x

e

v = - 8 π cos ⁡ π 8 x

A integral vai ficar:

∫ - 4 4 x sen ⁡ π 8 x d x = x ⋅ - 8 π cos ⁡ π 8 x - 4 4 - ∫ - 8 π cos ⁡ π 8 x d x

∫ - 4 4 x sen ⁡ π 8 x d x =

4 ⋅ - 4 8 π cos ⁡ π 8 4 - - 4 ⋅ - 4 8 π cos ⁡ π 8 - 4 - ∫ - 4 4 - 8 π cos ⁡ π 8 x d x

4 ⋅ - 4 8 π 0 - - 4 ⋅ - 4 8 π 0 — ∫ - 4 4 - 8 π cos ⁡ π 8 x d x

Para facilitar pelo menos um pouco nossa vida esses termos ali valem zero e só sobra a outra integral para calcular

∫ - 4 4 x sen ⁡ π 8 x d x = 0 - 0 - ∫ - 4 4 - 8 π cos ⁡ π 8 x d x

∫ - 4 4 x sen ⁡ π 8 x d x = ∫ - 4 4 8 π cos ⁡ π 8 x d x

Agora é só calcular essa integralzinha aqui,

∫ - 4 4 8 π cos ⁡ π 8 x d x

que é bemmm mais fácil que as ultimas ai.

Passo 4

Vamos tirar a constante para fora da integral

∫ - 4 4 8 π cos ⁡ π 8 x d x

8 π ∫ - 4 4 cos ⁡ π 8 x d x

8 π 8 π sen ⁡ π 8 x - 4 4

8 π 8 π sen ⁡ π 8 4 - 8 π sen ⁡ π 8 - 4

8 π 8 π 1 - 8 π - 1

8 π 16 π

128 π 2

Do passo anterior temos que

∫ - 4 4 x sen ⁡ π 8 x d x = ∫ - 4 4 8 π cos ⁡ π 8 x d x

logo

∫ - 4 4 x sen ⁡ π 8 x d x = 128 π 2

Voltando ao Passo 2, nós temos

∫ - 4 4 x 2 cos ⁡ π 8 x d x = 256 π - ∫ - 4 4 8 π sen ⁡ π 8 x 2 x d x

∫ - 4 4 x 2 cos ⁡ π 8 x d x = 256 π - 16 π ∫ - 4 4 x sen ⁡ π 8 x d x

Então substituindo aquela integral a gente tem

∫ - 4 4 x 2 cos ⁡ π 8 x d x = 256 π - 16 π 128 π 2

∫ - 4 4 x 2 cos ⁡ π 8 x d x = 256 π - 2048 π 3

Também do passo 2 a gente sabe que

I y = 2 ∫ - 4 4 x 2 cos ⁡ π 8 x d x

Então

I y = 2 256 π - 2048 π 3

I y = 30,9   m 4

Resposta

I y = 30,9   m 4

Ver Outros Exercícios desse livro