Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 15
A bobina tem uma massa de e se apoia contra a parede e o piso. Se o coeficiente de atrito estático em é , o coeficiente de atrito cinético é e a parede é lisa, determine a força de atrito desenvolvida em quando a força vertical aplicada ao cabo é .
Passo 1
O problema pede que encontremos a força de atrito em .
Vamos fazendo um diagrama de corpo livre, desse jeito:
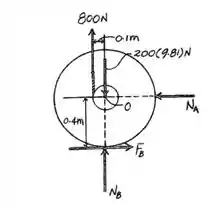
Então agora, vamos usar a equação de equilíbrio das forças no eixo :
Agora, no eixo :
E usando a equanção de equilíbrio para o momento a gente fica com:
E achamos:
Passo 2
E então, calculamos a :
Como é maior que , não ultrapassou o máximo, então:
Resposta
Exercícios de Livros Relacionados
6/47) Um bloco de massa m 0 é colocado entre a parede vertical e a extremidade superior , A , da barra esbelta uniforme de massa m . Se o coeficiente de atrito estático entre o bloco e a parede e tamb
6/44) Determine a distância s que a pintora de 90k g pode subir sem fazer com que a escada de 4m escorregue em sua extremidade inferior A . O topo da escada de 15k g tem uma pequena roldana e , no chã
6/43) As duas barras A C e B D são feitas do mesmo material . Determine o ângulo θ no qual a barra A C deslizará e faça um gráfico de θ em função do coeficiente de atrito estático μ s na faixa 0 ≤ μ s
6/37) O semicilindro homogêneo repousa sobre uma superfície horizontal e estásubmetido a uma força P aplicada a um cabo firmemente preso asua periferia . A força P é lentamente aumentada e mantida nor
6/39) A cabeça do grampo de marceneiro é soldada a seu eixo de diâmetro d e é projetada para prender a peça de trabalho A em seu lugar . O grampo é ajustado batendo inicialmente em sua cabeça com uma