Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 27
10.27 Determine a distância até o centroide da área transversal da viga; depois, ache o momento de inércia em relação ao eixo .
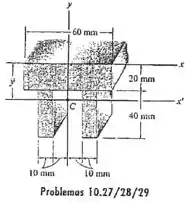
Passo 1
A distância , até o centroide, é dada pela fórmula:
Vamos separar essa área em 3 retângulos:
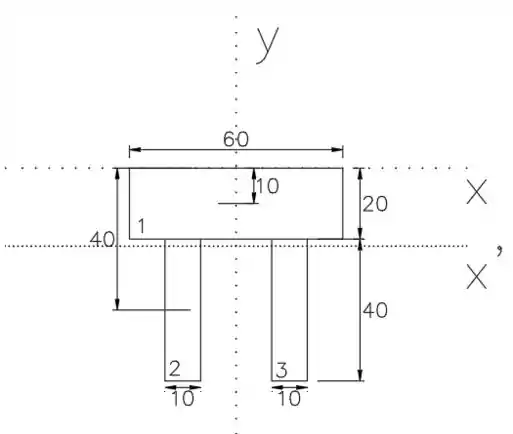
A distância até o centroide do primeiro é , já do segundo e terceiro é :
As áreas são iguais a:
Então seu centroide estará localizado em
Agora é só calcular o momento de inercia.
Passo 2
O centroide dos retângulos não coincide com o eixo que estamos usando para calcular o momento de inercia, então precisamos usar o teorema dos eixos paralelos. Vamos calcular o momento de inercia de cada retângulo e depois soma-los.
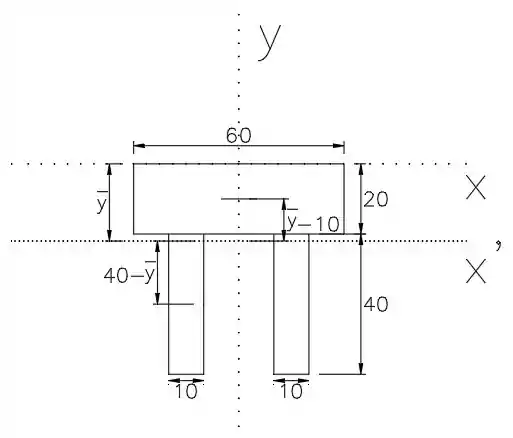
Pela tabel,a sabemos que o momento de inercia de um retângulo é igual a , usando o teorema dos eixos paralelos vamos ter que
Nós já descobrimos o valor de :
Para 2 e 3 o processo é o mesmo:
Nós já descobrimos o valor de :
Somando os três momentos obtemos o total: