Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 97
Determine a menor força na alavanca necessária para impedir que a roda gire se ela estiver sujeito a um torque de . O coeficiente de atrito estático entre a correia e a roda é . A roda está presa em seu centro, , por meio de um pino.
Passo 1
Marcando as forcas na ilustração, temos o seguinte:
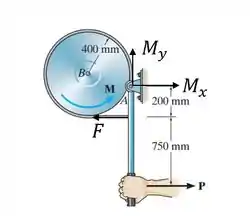
Passo 2
Como nosso sistema está em equilíbrio, a torque resultante é nulo. Considerando positivo no sentido anti-horario, temos:
Ponto :
Assim,
Agora vamos analisar a roda:
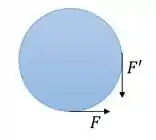
Usando aquela formulinha da teoria ():
Logo,
Repare que pegamos o ângulo no sentido anti-horario, por isso . Fazendo as contas:
Passo 3
Como queremos saber a força, podemos fazer torque com relação ao ponto , olha só:
Logo,
Substituindo os valores:
Fazendo as contas:
Resposta
Exercícios de Livros Relacionados
O coeficiente de atrito estático entre o tambor e a alavanca de freio é μ s = 0,4 . Sendo o momento M = 35N ∙ m , determine a menor força P que precisa ser aplicada à alavanca a fim de impedir que o t
Determine a menor força P necessária para empurrar o tubo E para cima no aclive. A força atua paralelamente ao plano e os coeficientes de atrito estático nas superfícies de contato são u A =0,2 , u B=
A viga A B tem massa e espessura desprezíveis e está sujeita a uma carga distribuída triangular. Ela é apoiada por um pino em uma ponta e por um poste com massa de 50k g e espessura desprezível na out
Determine a força de atrito na caixa de 40k g e a força normal resultante em sua posição x , medida a partir do ponto A , se a força é P=300N . Considere μ s = 0,5 e μ k = 0,2 .
O gancho por atrito é composto de uma estrutura fixa e de um cilindro de peso desprezível. Um pedaço de papel é colocado entre a parede e o cilindro. Se θ=20 º º, determine o menor coeficiente de atri