Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 28
10.28 Determine o momento de inércia da área da seção transversal em relação ao eixo .
Passo 1
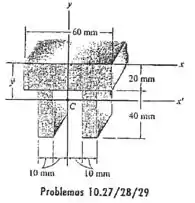
Faaaala! Aqui temos um exercício para achar o momento de inércia dessa seção em relação a . Repara que ele nos dá o eixo , que passa pelo centroide da seção e quer o momento de inércia em relação ao um eixo diferente, o .
Vamos separar essa área em 3 retângulos para simplificar a cara dessa seção
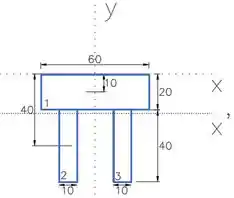
O momento de inércia total será a soma dos momentos de inercia desses três retângulos:
Pela tabela, sabemos que o momento de inércia de um retângulo é igual a , com sendo o comprimento do retângulo paralelo ao eixo em questão.
Como esse eixo não passa pelo centroide de nenhum retângulo, a gente vai precisar usar o teorema dos eixos paralelos. Fica assim:
Mas repara que a posição (ponto final e inicial) em relação a e a área dos retângulos 2 e 3 são iguais. Logo há uma simetria nessa seção, o que permite que a gente calcule as coisinhas referentes a ao retângulo 2 e multiplique o resultado por 2:
Bora calcular!
Passo 2
Da figura, temos:
é a distância entre o centroide da figura e o eixo . Para o primeiro é , já do segundo e terceiro é :
As áreas são iguais a:
Então nossa equação vai ficar: