Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 107
Se , determine a tração máxima desenvolvida na corrente e seu comprimento, a corrente tem uma massa por unidade de comprimento de .
Passo 1
O problema quer que a gente encontre a tração máxima na corrente e o comprimento dela.
Vamos começar fazendo um diagrama de corpo livre, assim:
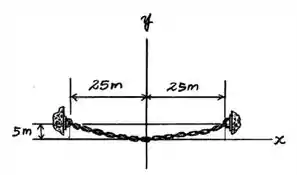
Onde o carregamento pode ser descrito como:
Perceba que a questão deu como unidade de passa por isso multipliquei pela gravidade para encontrar o peso.
Passo 2
Nós notamos que na figura do problema, é o ponto mais baixo do cabo, vamos pegar a segunda derivada da equação do cabo, logo:
Se nós consideramos , então , logo:
E integrando isso:
Vamos encontrar , pra isso a gente usa a condição inicial, de que na origem, e então:
Logo é igual a .
Ficamos com:
Agora, vamos dar uma ajeitada e tentar simplicar isso, calma, eu sei que parece muito estranho:
Agora lembra que , aí ficamos com:
Integramos mais uma vez para chegarmos na função não derivada:
Testando a equação na condição inicial, onde e , encontramos que:
Logo, ficamos com:
Aplicamos no ponto que é e para encontrarmos :
Resolvendo por tentativa e erro, conseguimos achar:
Passo 3
Tá quase acabando, mas antes da gente encontrar a força de tração máxima, temos que encontrar o ângulo máximo formado pela tração, podemos notar visualmente que isso ocorre em o que nos poupa muitos cálculos.
Para encontramos o ângulo é bom lembrarmos que a derivada é a tangente do ângulo formado em relação ao eixo, assim:
Sabemos que:
Então:
Finalmente, a tração máxima:
Passo 4
Por fim, a gente só precisa encontrar o comprimento da corrente, pra isso vamos fazer um diagrama de corpo livre:
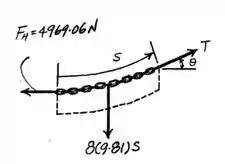
Agora, analizamos as forças nos dois eixos:
Eliminando o , a gente acaba encontrando:
Então igualamos a equação derivada:
Assim encontramos:
Substitumos o por , e obtemos a resposta: