Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 30
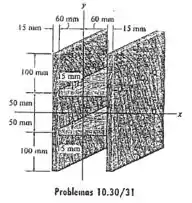
10.30 Determine o momento de inércia da área da seção transversal em relação ao eixo .
Passo 1
Falaa galerinha do RespodenAi, tudo beleza??
Saca só, o macete nesse exercício aqui, é a gente separar essa área da seção transversal em 4 retângulos, desse jeito ó:
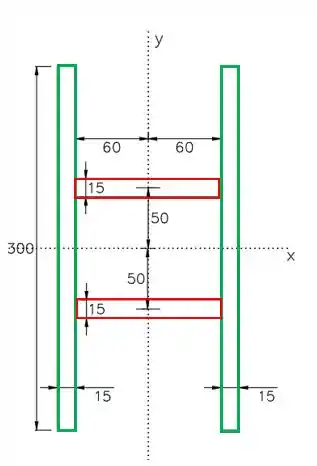
O momento de inércia total será a soma dos momentos de inercia desses quatro retângulos. Além disso, podemos observar que os momentos de inércia dos retângulos que estão na horizontal vão ser iguais, assim como os momentos de inercia dos que estão na vertical, pois eles tem as mesmas medidas e distâncias até eixo .
Belezoca, então bora descobrir esses momentos de inércia pra gente poder somar.
Passo 2
Sabemos que o momento de inércia em relação ao eixo do centroide de um retângulo é dado como:
Para os retângulos em verde, temos que o eixo do seu centroide coincide exatamente com o eixo da seção transversal da figura, de modo que para um retângulo verde, teremos:
Como temos dois retângulos verdes com o mesmo momento de inércia em relação a , teremos que:
Passo 3
Iradoso, agora para os retângulo em vermelho, temos que o eixo do seu centroide, não coincide com o eixo que desejamos encontrar o momento de inércia. Isso quer dizer que vamos precisar encontrar seu momento de inércia através do teorema dos eixos paralelos, dado como:
Onde é o momento de inércia em relação ao centroide, enquanto que é a distância entre os eixos paralelos e a área da figura. Como é tabelado e dado como:
E é dado por , obtemos que para um retângulo em vermelho, seu momento de inércia será:
Logo:
E como são dois retângulos vermelhos com o mesmo momento de inércia, teremos:
Passo 4
Maravilha, então agora que temos o momento de inércia de todas as figuras, é só a gente somar algebricamente, de maneira que o momento de inércia da área da seção transversal em relação ao eixo será dado como:
Portanto: