Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 26
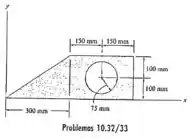
10.32 Determine o momento de inércia da área da seção transversal em relação ao eixo .
Passo 1
Fala! Queremos o momento de inércia dessa área composta.
Vamos separar essa área em 3 pedaços, o triângulo,o retângulo e a cicunferência:
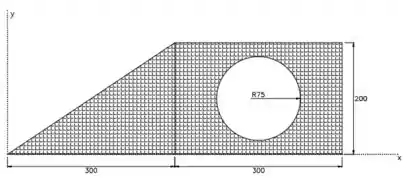
O momento de inércia total será a soma dos momentos de inercia do triângulo e do retângulo, menos o momento de inercia da circunferância:
Pela tabela, sabemos que os momentos de inércia dessas formas são:
O momento de inercia, já aplicando o terorema dos eixos paralelos, fica assim:
Onde é a distância do centroide da figura até o eixo .
Passo 2
A largura da base e a altura tanto do retângulo como do triângulo, o exercícios nos dá. A distância até o centroide de cada retângulo é achada só dividindo a altura dele por 2:
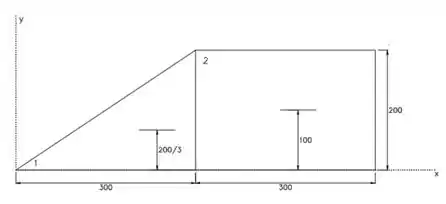
Da imagem, podemos perceber que:
Para achar para o triângulo, precisamos lembrar que sei centroide fica a um terço da base. Aí a gente precisa dividir a altura dele por 3:
Passo 3
Olhando para a circunferência:
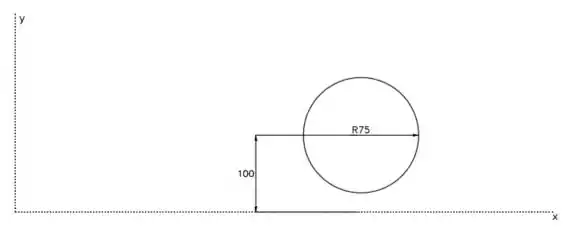
A área fica:
Passo 4
Vamos cacular o momentos de inercia separados, para não ficarmos com uma equação gigante e ter perigo de se perder no meio das contas.
Como a base do triângulo (segmento paralelo a ) é e altura é , o momento de inércia dele fica:
Para o retângulo, o segmento paralelo a é o de comprimento . Essa é a base e altura é :
E para a circunferência de raio
Então, somando o retângulo e triângulo e subtraindo a circunferência: