Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 71
Blocos uniformes com um comprimento , e massa são empilhados uns sobre os outros, com cada bloco ultrapassando o outro por uma distância , conforme mostrado. Mostre que o número máximo de blocos que podem ser empilhados dessa maneira é .
Passo 1
O problema pede que encontremos o maior número de blocos sendo que .
Pense assim, quando o centro de massa dos blocos ultrapassar o tamanho do bloco de baixo (), a estrutura deixara se ser estável, porque a força peso atua no centro de massa.
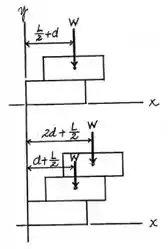
E o centro de massa é dado por:
E pra facilitar, vou dar um dica importante: Quando o corpo é simétrico em um eixo e o corpo tem sua massa distribuída uniformemente, o centro de massa será no centro do corpo em relação ao eixo, a imagem agora vai facitilar muito sua vida:
Passo 2
Agora vamos calcular os centros de massa de cada bloco, vamos considerar os bloco de baixo pra cima , e respectativamente, então, vamos para calculo:
Então notamos que:
Agora, vamos calcular o centro de massa para algumas quantidade de blocos, mas apenas dos blocos acima do primeiro bloco, pra facilitar logo vamos usar o peso , ao invés de da massa:
A gente pode notar a sequência de resultados e generalizar:
Passo 3
Agora vamos usar essa generalização para ver até onde a estrutura continuará estável, ou seja, o centro de massa não pode ultrapassar .