Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 42

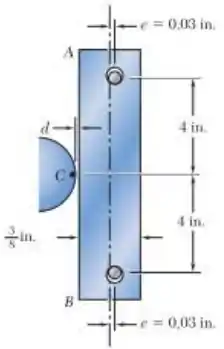
10.42: Para o Problema 10.41, determine a distância d necessária para a qual a barra entrará em contato com o ponto C quando a temperatura aumentar em 120 ° F .

3 8 × 3 8 i n . De lado e é suspensa por pinos a uma distância fixa entre si e localizados a uma distância e = 0,03 i n .   Do eixo geométrico da barra. Sabendo que na temperatura T 0   os pinos estão em contato com a barra e que a força na barra é zero, determine o aumento na temperatura para o qual a barra entrará em contato com o ponto C se d = 0,01 i n . Use E = 29 × 10 6 p s i e o coeficiente de expansão térmica α = 6,5 × 10 - 6 / ° F )

Passo 1

E ai gurizada tudo certo? O enunciado pede que a gente determine o aumento na temperatura. Vamos começar calculando a área e a inércia, vem comigo :D

A = 3 8 3 8 = 0,140625 i n 2

I = 1 12 3 8 4 = 1,64795 × 10 - 3 i n 4

E I = 29 × 10 6 1,64795 × 10 - 3 = 47,791 l b ∙ i n 2

P e r = π 2 E I L 2 = π 2 47,791 8 2 = 7370 l b

Passo 2

O alongamento é dado por:

α L Δ T - P L E A = 0

P = E A α Δ T = 29 × 10 6 0,140625 6,5 × 10 - 6 120 = 3181 l b

Calculando a deflexão temos:

d = y m a x = e sec ⁡ π 2 P P e r - 1 = ( 0,03 sec ⁡ π 2 3181 7370 - 1 = 0,03 sec ⁡ 1,03197 - 1 = 0,03 0,94883                

d = 0,0285 i n .

Resposta

d = 0,0285 i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

σ e = 250 M P a e E = 200 G P a
Uma coluna de 7,8m de comprimento efetivo deve suportar uma carga centrada de 1100 kN. Sabendo-se que σ e = 345 M P aeE = 200 G P a ,s e l e c i o n ar o perfil laminado de aço, com abas largas e de d
Uma coluna de comprimento efetivo 4,4m deve suportar uma carga centrada de 1150kN. Sabendo-se que σ e = 350M P aeE = 200 G P a , selecionar o perfil laminado de aço, com abas largas, de dimensão nomin
Uma coluna de 8,4 m de comprimento efetivo deve suportar uma carga centrada de 780 kN. Sabendo que σ e = 250M P aeE = 200G P a , selecionar o perfil laminado de aço, com abas largas e de dimensão nomi
A barra A B é livre em sua extremidade A e engastada em sua extremidade B . Determinar a carga centrada admissível P , quando a liga de alumínio usada é: (a) 6061-T6 e (b) 2014-T6