Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 106

σ e = 250   M P a   e E = 200   G P a

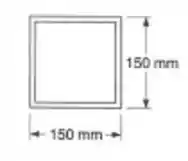
Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o tubo mais leve que pode ser usado, para isso vamos trazer os dados do enunciado , partiu?

b o = 150 m m       b i = b o - 2 t       A = b o 2 - b i 2

I = 1 12 b o 4 - b i 2

L e = 7,8 m             P = 260 k N

σ γ = 250 M P a             E = 2000 P a

Passo 2

Para o aço temos que:

C c = 2 π 2 E σ γ = 2 π 200000 250 = 125,7

Considerando as seguintes informações temos:

t = 12 m m             b i = 126 m m       A = 150 2 - 126 2 = 6624 m m 2

A inércia é dada por:

I = 1 12 150 4 - 126 4 = 21,18 × 10 6 m m 4 .

r = I A = 55,6 m m .

L e r = 7800 55,6 = 140,3 > C c

E a tensão pode ser calculada como:

σ μ = π 2 E 1,92 L e r 2 = 52,23 M P a

Passo 3

Temos que a força P é:

P μ = σ μ A = 52,23 6624 = 346   k N

P μ   é   a p r o x i m a d a m e n t e   p r o p o r c i o n a l   a   t

t 12 = 260 346                 t ≈ 9,02 m m .

Passo 4

Tentamos agora os seguintes dados:

  t = 9 m m     b i = 132 m m   A = 5076 m m 2

I = 1 12 150 4 - 132 4 = 16,888 × 10 6 m m 4

r = I A = 57,68 m m

L e r = 7800 57,68 = 135,23 > C c

E a tensão é dado por:

σ μ = π 2 E 1,92 L e r 2 = 56,2   M P a .

P μ = σ μ A = 56,2 5076 = 285,3 k N > 260 k N

t = 9 m m

Resposta

9 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma coluna com 4,5m de comprimento de flambagem deve suportar uma carga centrada de 900k N . Sabendo que σ E = 345M P a e E = 200G P a por meio do método das tensões admissíveis escolha o perfil de me
Uma carga vertical P de 11k i p é aplicada no ponto médio de uma aresta da seção transversal quadrada de um elemento de aço comprimido AB,o qual é livre no topo A e fixo em sua base B . Sabendo que pa
A linha de ação da força axial de 310k N é paralela ao eixo geométrica da coluna AB e intercepta o eixo x em x = e . Usando E = 200 G P a , determine (a) a excentricidade e quando a deflexão no ponto
Uma coluna retangular com 4,4m de comprimento de flambagem é feita de madeira laminada colada. Sabendo que, para o grau de madeira utilizado, a tensão admissível à compressão paralelas às fibras ajust
Uma carga axial P é aplicada à haste de aço AB com 32 mm de diâmetro conforme mostrada. Para P = 37k N e e = 1,2m m , determine (a) a deflexão do ponto médio da haste em C, (b) a tensão máxima na hast