Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas fundamentais - Ex. 5
10.5 Determine o momento de inércia da área da seção transversal da viga em relação aos eixos centroidais e .
Passo 1
Falaaa! A gente quer o momento de inércia em relação ao eixo e ao eixo . Essa seção é diferentona, mas a gente pode dividir em figuras mais simples para calcular o momento de inércia.
Vamos dividir essa área em 3 retângulos:
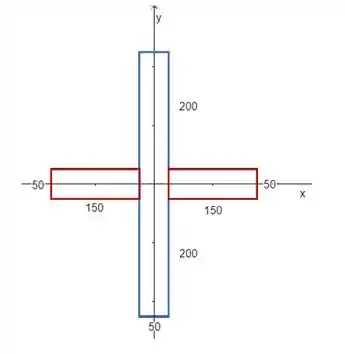
O momento de inércia total será a soma dos momentos de inercia desses três retângulos:
Repara que temos 2 retângulos iguais, esses em vermelho. Além de eles terem seus tamanhos iguais a distância de seus centroides até o eixo é igual, por essa razão, só precisamos calcular o momento de inércia de um e multiplicar o resultado por 2.
Sendo 1 o retângulo vermelho a direita e 2 o azul ao meio.
O momento de inercia de um retângulo, em relação ao eixo , é igual a . Onde é a dimensão do segmento do retângulo paralelo a . E é a dimensão do outro segmento do retângulo.
E como o centroide dos três retângulos passam pelo eixo , não será necessário usar o teorema dos eixos paralelos. Aí ficamos assim:
Substituindo os dados que a gente tem na figura:
Obs: o gabarito está com a resolução errada, porque ele esqueceu de usar esse dois ali na multiplicação, tá? Aqui estamos certinhos.
Passo 2
Da mesma forma que para o eixo , o momento de inercia para o eixo será a soma do momento de inercia dos três retângulos.
O momento de inercia de um retângulo, em relação ao eixo , é igual a . Onde é a dimensão do segmento do retângulo paralelo a . E é a dimensão do outro segmento do retângulo.
Como o centroide, do retângulo do meio, passa pelo eixo , não será necessário usar o teorema dos eixos paralelos para esse retângulo, já para os outros dois sim:
Mas aqui a gente pode usar a simeteria de novo, isso porque os retângulos vermelhos são iguas e têm a mesma distância dos seus centroides até o eixo . Aí a gente calcula só o momento de um deles e multiplica por 2:
é a área do retângulo e é a distância do centroide do retângulo até o eixo . Vamos calcular essas coisinhas!
Passo 3
Precisamos da área do retângulo que está na lateral, assim como a distância de seu centroide até o eixo .
A distância do centroide até o eixo é:
A equação va ficar assim: