Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas fundamentais - Ex. 8
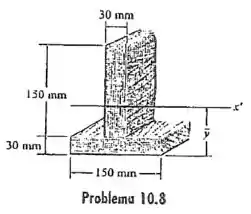
10.8 Determine o momento de inércia da área da seção transversal da viga em relação ao eixo passando pelo centroide da seção transversal.
Passo 1
Fala ai galerinha do RespondeAí, tudo beleza?
Saca só, nesse exercício aqui, o enunciado quer que a gente encontre o momento de inércia da seção transversal de uma viga que passa pelo seu centróide, pra isso, podemos primeiro dividir a figura em duas partes, tal que:
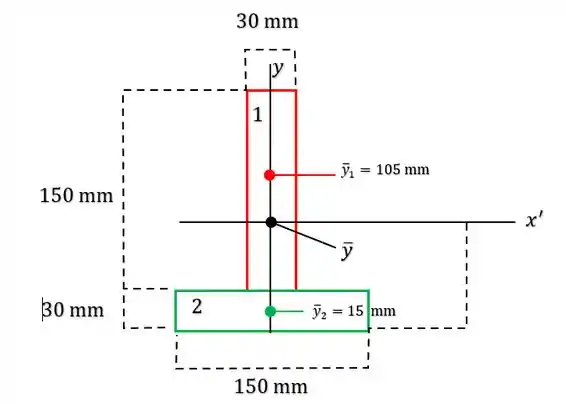
Onde e são as componentes em do centróide da figura e da figura respectivamente. Sendo assim, podemos calcular logo de cara, a componente do centróide da figura toda, onde o eixo está passando, através da fórmula:
Isso quer dizer que seu centroide estará localizado em:
Logo:
Agora podemos ir calcular o momento de inércia em relação ao eixo que passa por esse centróide.
Passo 2
Show de bolinhas, agora pra gente calcular o momento de inércia da figura em relação ao centróide, podemos calcular o momento de inércia de cada figura separadamente e depois somar, ou seja, dado que e são os momentos de inércia de cada figura em relação ao eixo , o momento total vai ser a soma dos dois:
Belezinha, então bora lá encontrar esses momentos de inércia de cada figura.
Para a primeira figura, teremos um retângulo em que o momento de inércia em relação ao seu próprio centróide, será tabelado e dado como:
Onde é a base do retângulo e é a altura. MAAASSS, queremos o momento de inércia em relação ao eixo e não em relação ao eixo que passa pelo centróide da figura , então pra resolver isso podemos aplicar o teorema dos eixos paralelos, dado como:
Em que é distância entre os eixos, ou melhor, nesse caso é a distância entre os centróides:
Sendo assim:
Iradoso, agora se a gente fizer o mesmo procedimento para a figura , vamos obter que:
Onde vai ser dado como:
Segue que:
Passo 3
Belezera, como descobrimos os valores dos dois momentos de inércia, podemos somar e encontrar o momento resultante em torno de , dado como:
Portanto: