Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 33
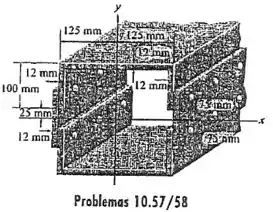
10.58 Determine o momento de inércia da seção. A origem das coordenadas está no centroide .
Passo 1
Falaaa! A gente quer o momento de inércia em relação ao eixo . Essa seção é diferentona, mas a gente pode dividir em figuras mais simples para calcular o momento de inércia.
Vamos dividir essa área em 8 retângulos:
Mas perceba que temos:
2 retângulos iguais, na horizontal, que chamamos de 1
4 retângulos iguais na vertical, que chamamos de 2
e 2 retângulos iguais na vertical, que chamamos de 3
Além de eles terem seus tamanhos iguais a distância de seus centroides até o eixo é igual, por essa razão, só precisamos calcular 3 momentos de inercia diferentes e multiplicar pela quantidade de retângulos de cada momento de inercia.
O momento de inercia total, será a soma do momento de inercia desses oito retângulos.
O momento de inercia de um retângulo, em relação ao eixo , é igual a . Sendo a dimensão do segmento paralelo ao eixo .
Como o centroide do retângulo 1 coincide com o eixo , não será necessário usar o teorema dos eixos paralelos para ele, já para 1 e 2 sim.
Esse é a área da figura, e é a distância entre e o centroide da figura.
Passo 2
Precisamos da área dos retângulos 2 e 3:
e
A distância do centroide até o eixo achamos olhando para a imagem, a gente observa que:
e
A base e a altura do retângulo 1 nós podemos observar na imagem:
Passo 3
Pra não ficar com uma equação muito grande vamos calcular os momentos de inercia de 1, 2 e 3 separadamete e depois jogá-los na nossa fórmulinha:
Rentângulos 1:
Rentângulos 2:
Rentângulos 3:
Agora substituindo na equação do momento de inercia total: