Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 59
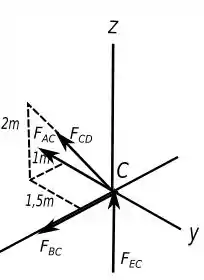
Determine a força em cada membro da treliça especial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em e . Considere . Dica: A reação de apoio em atua ao longo do membro Por quê?
Passo 1
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração, mas sim de compressão.
Vamos analisar cada ponto separadamente e utilizar as equações de equilíbrio referentes as forças em cada direção.
Para isso vamos usar as componentes das forças em cada direção, para isso vamos transformar essas forças em vetores, para isso basta multiplica-las por seus respectivos vetores unitários.
Passo 2
Vamos começar analisando o ponto , abaixo tem um diagrama de forças que mostra a situação.
Usando as forças transformadas em vetores:
Resolvendo esse sistema de equações encontramos:
Passo 3
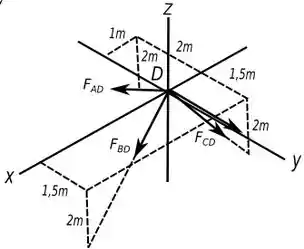
Vamos começar analisando o ponto , abaixo tem um diagrama de forças que mostra a situação.
