Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 59
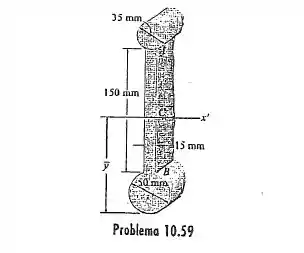
Determine o momento de inércia da área da seção transversal da viga em relação ao eixo que passa pelo centroide da seção transversal. .
Passo 1
Fala pessoal! Vamos lá!
Seguinte para calcular o momento de inércia dessa figura, temos que ter em mente que temos 3 figuras: 2 círculos e um retângulo. Logo, aos termos 3 figuras e também um eixo paralelo passando pelo centroide de da figura principal, utilizaremos o teorema dos eixos paralelos.
Para determinar o teorema dos eixos paralelos temos que satisfazer para cada figura a seguinte fórmula:
Significa que iremos calcular o momento de inércia de cada figura, a sua área, determinar a distância de cada figura até o eixo e por final executar o somatório.
Inicialmente temos esta situação:
Irei adicionando mais informações ao desenho assim que avançarmos nos passos.
Passo 2
Como dito anterior mente, vamos ter que calcular algumas coisas. Vamos começar com o cálculo das áreas:
Cálculo da área do primeiro círculo:
Cálculo de área do retângulo:
Cálculo de área do segundo círculo:
Passo 3
Após determinar a área de cada figura, vamos calcular o momento de inercia de cada uma delas em relação aos eixos que passam pelos seus próprios centroides.
Calculando o momento de inércia do primeiro círculo, por definição o momento de inercia é o seguinte:
Calculando o momento de inerciado retângulo, por definição:
Vemos que é o valor da dimensão do retângulo que é paralela ao eixo .
Calculando o momento de inércia do segundo círculo:
Passo 4
Agora vamos para o momento chave da questão, determinar a distância do centro de cada figura até o eixo , para isto, é muito bom determinar o eixo como ponto e partir disto executar os raciocínios.
Primeiro vamos tratar do primeiro círculo:
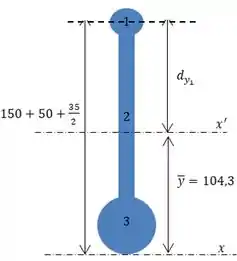
Seguinte, temos a soma do raio , do retângulo e o raio resultando no comprimento do eixo até o centro do nosso circulo 1.
Para termos a distância será a diferença deste somatório com a distância do centroide da figura ao eixo .
Para nosso retângulo:
Vamos encontrar o centro do nosso retângulo, que fica . Vamos lembrar que estamos tratando o eixo como ponto zero, logo vamos somar o diâmetro do círculo 3 e teremos o comprimento do eixo até centro do retângulo:
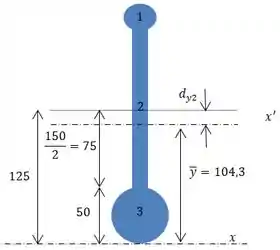
Executando a diferença do comprimento com o centroide temos :
Para círculo 3, será a distância do centro do círculo até centroide:
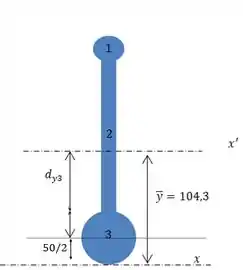
Executando a diferença do raio com o centroide, temos:
Passo 5
Agora ficou simples, basta substituirmos todos os cálculos efetuados na seguinte fórmula para cada figura e executar o somatório:
Para primeiro círculo:
Para o retângulo:
Para segundo círculo:
Somando os três, teremos nosso resultado final: