Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 29
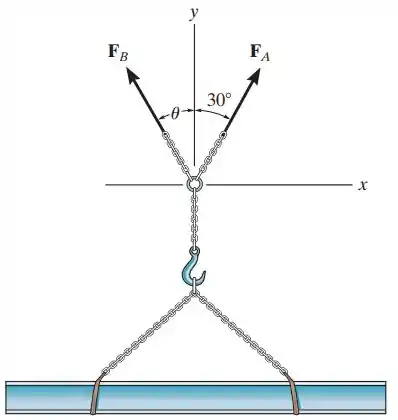
2.29. A viga deve ser içada usando-se duas correntes. Se a força resultante for de , orientada ao longo do eixo y positivo, determine as intensidades das forças que atuam em cada corrente e o ângulo θ de para que a intensidade de seja mínima. atua a 30° do eixo y, como mostra a figura.
Passo 1
Faaala! A gente precisa achar e , e sabendo que
- precisa ser mínima.
- a força resultante entre e está na direção de e vale
Vou começar com um bizu: para que seja mínima, o ângulo entre deve ser 90°.
Se a gente já sabe que o ângulo que faz com é , por isso o ângulo que faz com é , aí soma desses ângulos dá . Então:
Aí para descobrir o valor das forças, vamos analisar os vetores das forças. Bora lá!
Passo 2
A gente pode fazer um esquema dos nossos vetores , e , e aí poderemos usar a lei dos paralelogramos, vou desenhar isso.
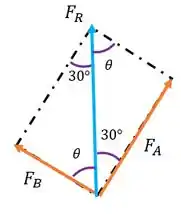
A gente acha essa outra localização dos nossos ângulos sabendo que ângulos opostos do paralelogramo precisam ser iguais e que a soma de ângulos internas de um triângulo é .
E lembra também que . O que faz com que esses triângulos que formam o paralelogramo sejam triângulos retângulos. Não acredita? Vamos desenhar um triângulo desses. Mas repara que lados paralelos tem mesmo tamanho. Aí fica assim:
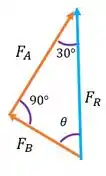
Se , e já temos o outro ânguo conhecido de , o último ângulo precisa ser de para que a soma desses ângulos seja .
Passo 3
Agora vamos calcular as intensidades das forças usando trigonometria
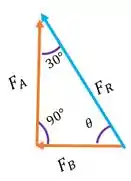
é nossa hipotenusa, é o cateto adjacente a enquanto o cateto oposto, aí para descobrir o valor deles, fazemos: