Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 39
2.39. Determine a intensidade de e sua direção θ, de modo que a força resultante seja direcionada verticalmente para cima e tenha a intensidade de .
Passo 1
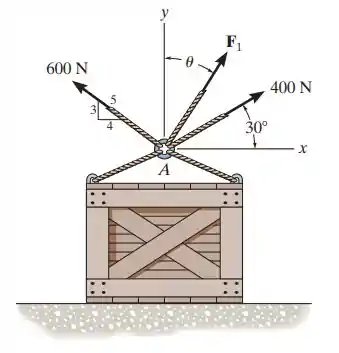
O exercício pede para que a gente calcule a intensidade de e sua orientação , para que a força resultante esteja no sentido positivo de e tenha o valor de
Daqui a gente pode tirar duas coisas. Se nossa resultante está somente no eixo , a componente em dela é zero, e componente vai ser igual ao seu módulo, assim
Então, o que podemos fazer é achar expressões para e e igualar a esses valores. Assim teremos duas equações, suficientes para achar nossas duas incógnitas.
Vem!
Passo 2
Vamos determinar a componente de no eixo x. Aí a gente decompõe nossas forças nesse eixo e soma.
A componente de vai ser
Usamos seno porque nosso ângulo está oposto ao eixo .
O contrário acontece para . O ângulo de está coladinho em . Então vamos usar cosseno na componente em :
Para , a gente vai usar as relações trigonométricas do triângulo retângulo.
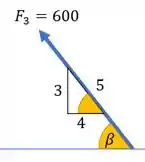
Vamos chamar o ângulo que essa força faz com a horizontal de . Como ele está coladinho em , nossa componente em fica
Ela é negativa, porque está no sentido negativo de . Lembrando que
Temos:
Passo 3
Achamos a expressão para a resultante somando todas as componentes em que achamos:
Lembra que
Daí tiramos
Passo 4
Agora a gente calcula as componentes no eixo y
Para , como está colado em :
Para o ângulo de está oposto a , então:
E para , está oposto a também
Sendo que pelo triângulo retângulo que orienta nossa forcinha:
Então:
Todas ficam positivas porque todas estão no sentido positivo de .
Passo 5
A resultante nesse eixo fica:
Lembrando que
Passo 6
Temos essas duas equações:
Tem algumas formas de resolver esse sistema, uma delas é essa aqui:
Elevamos as equações ao quadrado e somamos para sumir com o θ, afinal
Passo 7
Agora podemos usar para descobrir θ