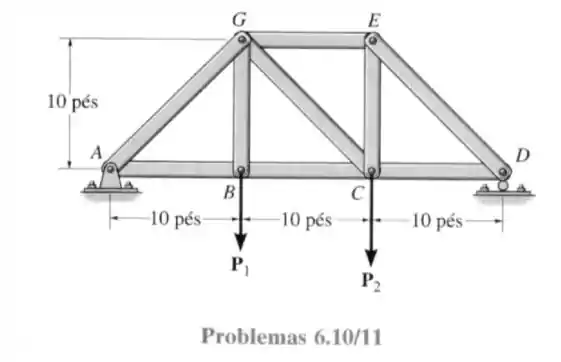
11- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Considere que e .
Passo 1
Da mesma forma que fizemos na questão passada calculando as reações, vamos também começar calculando as reações nos apoios, sabendo que não haverão reações horizontais teremos o seguinte diagrama de forças abaixo.
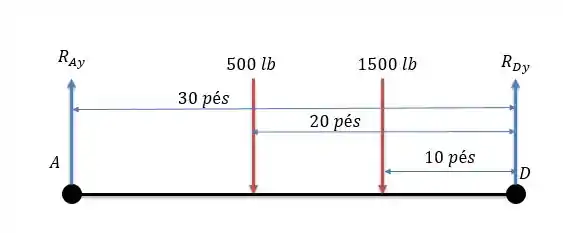
A somatória das forças verticais nesse diagrama de forças nos daria:
E a somatória dos momentos em seria igual a:
Logo o apoio em teria reação vertical igual a:
Passo 2
Agora podemos calcular as forças presentes na junta .
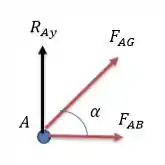
Onde será calculado pelo triângulo retângulo a qual ele pertence que valerá:
Fazendo a somatória das forças verticais teremos:
Logo:
Por representarmos a força saindo do nó então o sinal negativo nos diz que essa força é uma força compressiva.
Agora fazendo a somatória das forças horizontais nós teremos:
Força trativa.
Passo 3
Agora vamos analisar as forças no nó , pois é a que temos a possibilidade de achar todas as forças nessa momento.
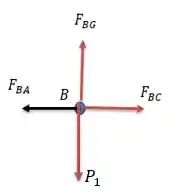
Fazendo a somatória das forças verticais nós teremos:
E a somatória das forças horizontais:
Força essa sendo uma força trativa.
Passo 4
Agora vamos analisar as forças para o nó .
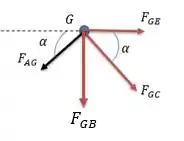
Fazendo a somatória das forças verticais:
Agora para a somatória das forças horizontais temos:
Força compressiva.
Passo 5
Agora indo para a junta :
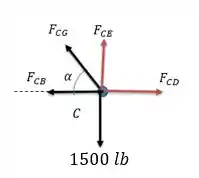
Fazendo a somatória das forças horizontais temos:
Substituindo os valores temos:
Agora fazendo a somatória das forças verticais:
Passo 6
Agora para o nó :
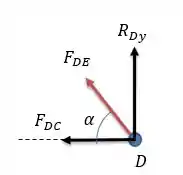
Fazendo a somatória das forças horizontais:
Força compressiva.