Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 11

11- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo x .

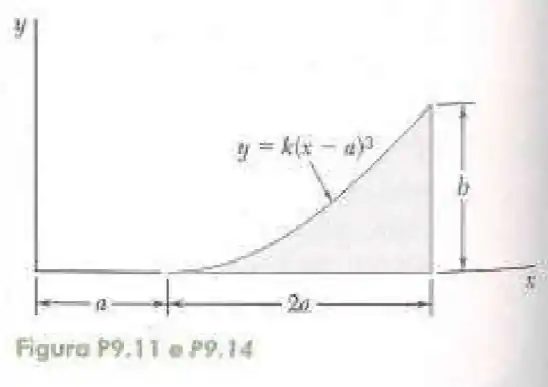
Passo 1

Vamos fazer a integral em x fazendo o elemento de área por linhas verticais, logo o termo de 1 / 3 será utilizado por conta desses elementos terem posições diferentes em x .

Deixando a integral da inércia da seguinte maneira:

I x = 1 3 ∫ a 3 a y 3   d x

Onde k   será encontrado aplicando o ponto de ( 3 a , b ) na equação dessa curva:

b = k 3 a - a 3

k = b 8 a 3

Então a integral da inércia será:

I x = 1 3 ∫ a 3 a b 8 a 3   x - a 3   3   d x

Isso nos dá:

I x = b 3 1536 a 9 ∫ a 3 a x - a 9   d x

Isso pode ser feito como:

I x = b 3 1536 a 9 x - a 10 10 a 3 a

I x = b 3 1536 a 9 3 a - a 10 10 - 0 10

I x = 2 10 a b 3 15360 = a b 3 15

Resposta

I x = a b 3 15

Ver Outros Exercícios desse livro