Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 55
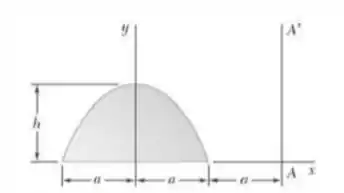
Determine o volume do sólido gerado pela rotação da área parabólica mostrado na figura em torno do eixo , do eixo .
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o volume gerado pela rotação da área parabólica em torno de dois diferentes eixos. Para isso, vamos utilizar o teorema de Pappus para o volume. Primeiro, precisamos encontrar a área da parábola, dada por:
E paraa , temos:
Passo 2
Agora, vamos usar o mesmo teorema de pappus:
Passo 3
Por fim, para a rotação em torno do eixo , vamos utilizar o mesmo teorema, entretando, mudaremos a distância para o eixo, dada agora por:
Vamos substituir no teorema, lembrando que vamos usar a mesma área encontrada anteriormentre. Fica assim:
Resposta
Exercícios de Livros Relacionados
Mostre que, para uma pirâmide regular de altura h e n lados n = 3 ,4 ,… , o centroide do volume da pirâmide está localizado a uma distância h / 4 acima da base.
Determine o centróide do sólido gerado pela revolução da parte da curva senoidal mostrada na figura em torno do eixo x .
Determine o centróide do volume obtido pela rotação da área sombreada da figura sobre o eixo x .
Determine o centroide da seção mostrada na figura, que foi obtida pelo corte de um tubo circular fino por dois planos inclinados.
Depois de nivelar um lote, um construtor coloca quatro estacas para indicar os cantos da base para uma casa. Para prover uma base nivelada firme, o construtor coloca um mínimo de 75 mm de brita abaixo