Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 59

Determine a capacidade, em litros, da poncheira mostrada se .

Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o volume, em litros, da figura. Para isso, vamos utilizar o teorema de Pappus para volume. Primeiro, vamos dividir a vista frontal da nossa figura em duas. Fica assim:

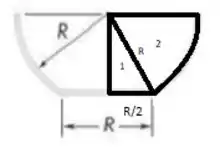
Agora, precisamos encontrar o valor da altura. Vamos usar o teorema de pitágoras:

Passo 2

Depois, sabemos que os centroides dessas figuras são conhecidos pois temos um triângulo retângulo e um arco de circunfência. Estes são dados por:

Substituindo:

Para o arco de circunferência:

Passo 3

Por fim, vamos usar a fórmula do teorema de pappus, para isso precisamos da área das figuras e da distância do eixo de rotação para o centro de massa de cada “projeção”:

Substituindo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centróide do sólido obtido pela rotação da área sombreada da figura em torno da linha x = h .

Determine por integração direta os valores de x - para os dois sólidos obtidos passando-se um plano de corte vertical através da forma dada na Fig. 5.21. O plano de corte é paralelo à base da forma da

Sabendo que dois topos iguais foram removidos da esfera de madeira de diâmetro 250 mm, determine a área total da superfície da parte restante.

Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e h .

Determine o centroide do sólido obtido pela rotação da área sombreada da figura em torno do eixo x .