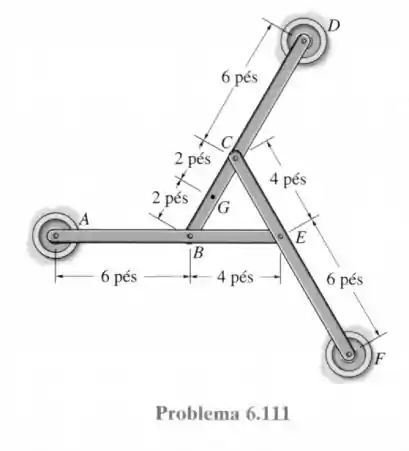
111- Os três elementos conectados por pinos mostrados em vista superior sustentam uma força para baixo de em . Se apenas forças verticais são sustentadas nas conexões e e nos blocos de apoio e , determine as reações em cada bloco.
Passo 1
Note que a questão facilitou nossa vida dizendo que todas as forças (nos pinos e nos blocos ) são verticais, além da força peso. Isso faz com que seja possível desenhar os diagramas de forças nas três barras da seguinte forma.
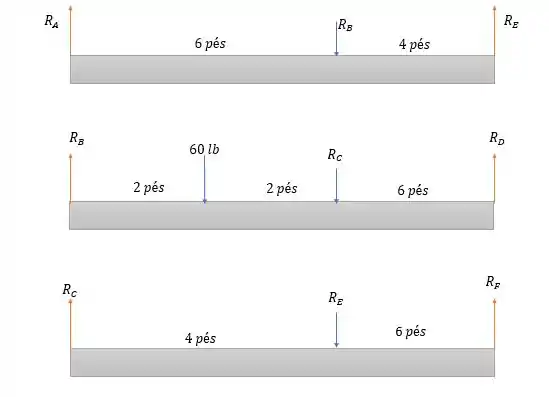
Onde a questão pede para resolvermos e .
Passo 2
Para a primeira barra indo de cima para baixo a somatória das forças nos dará:
E a somatória dos momentos em nos dará (é mais inteligente deixar em uma equação só e tratar as outras como variáveis intermediárias).
Agora para a segunda barra temos a somatória das forças igual a:
E a somatória dos momentos em igual a:
Agora para a terceira barra a somatória das forças:
E a somatória dos momentos em :
Passo 3
Substituindo o valor de de em temos:
Agora substituindo o valor de de em temos:
Logo a equação pode ser escrita como:
Porém como então:
Dessa forma: