Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.3 - Ex. 2
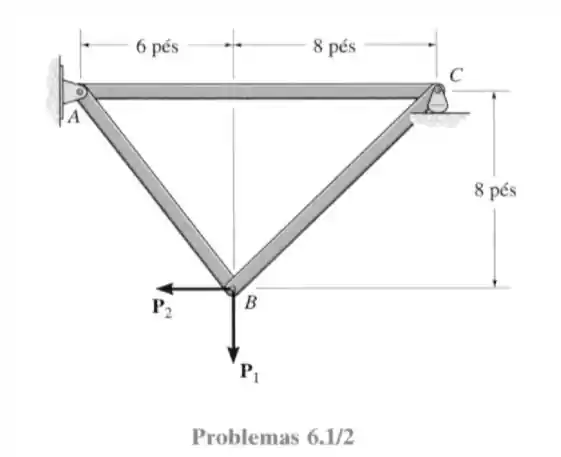
2- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Considere que e .
Passo 1
Então meu engenheiro(a) brabo(a).
A primeira medida a se tomar em uma questão como essa é de calcular as reações nos apoios (no caso nos apoios e ):
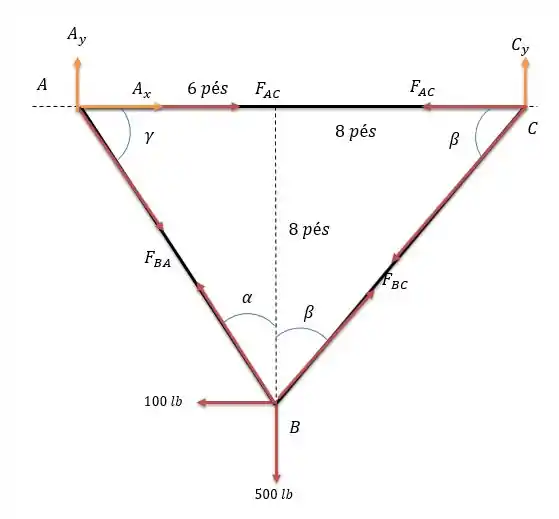
Sabendo que da questão anterior que:
E considere que as forças que passam sobre os elementos são de tração, isso é se temos uma força de tração sendo imposta pela barra . Pois é uma força de reação.
Fazendo a somatória das forças ativas no sistema (forças externas e reações nos apoios) nós teremos:
Para a somatória das forças em ser nula nós temos:
Agora para as forças ativas verticais:
Agora a somatória dos momentos em :
Isso dá:
Passo 2
Agora vamos fazer a somatória das forças no nó .
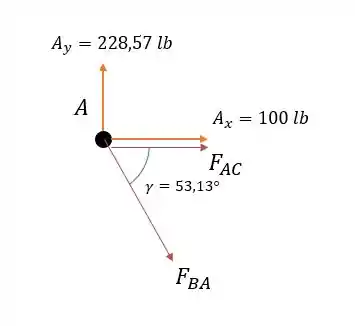
Fazendo a somatória das forças verticais teremos:
Então temos uma força de tração. Pois lembre que é uma reação da barra.
Agora pela somatória das forças horizontais no nó :
O que dá
O que será uma força compressiva.
Passo 3
Agora podemos encontrar a força na barra pelo nó ou pelo , vamos para o nó .
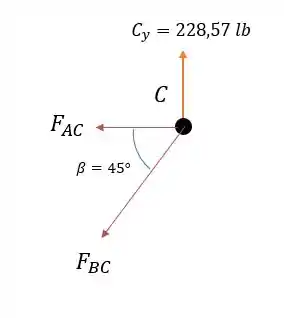
Fazendo a somatória das forças verticais no nó temos:
Isso dá:
O que é uma força trativa, já que deu um valor positivo.
Fizemos as duas questões de modo um pouco diferente para que você escolha o que é mais confortável para seu entendimento. Uma pode ser mais trabalhosa do que a outra porém deixar todas as forças de reação calculadas pode ser mais interessante para quem está começando do que já ir direto para a abordagem de cálculo por nós, pois essa de a força na barra ser uma força de reação pode ser um tanto confusa pra quem inicia.
O macete é pensar, cara que aponta para cima tende a tracionar ou comprimir a barra , tracionar, mas por que não vemos isso na prática pois existe uma que reage a isso.