Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.4 - Ex. 7

4.7. Determine a intensidade, a direção e o sentido do momento da força em A em relação ao ponto P.

Passo 1

Vamos começar desenhando o diagrama do corpo livre.

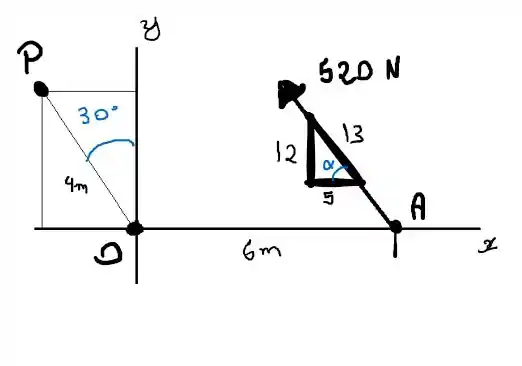
Passo 2

Muito bem, o momento de uma força é definido por

M = F ⋅ d

Onde

M = Momento

F =   Força

d = distância

Para calcular vamos decompor a força nos eixos x e y , e aí poderemos tratar como duas forças distintas, então ficamos com

M = M x + M y

Passo 3

Vamos calcular

M x = - 520 ⋅ cos ⁡ α ⋅ ( 4 ⋅ cos ⁡ 30 ° )

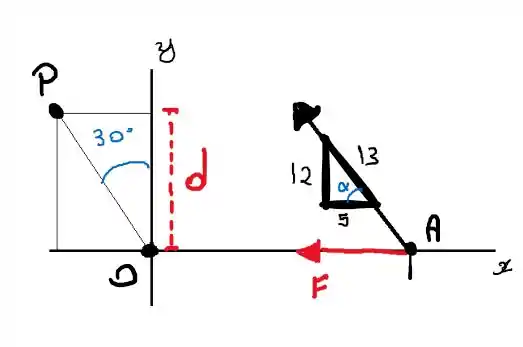
Mas pelo triângulo temos

cos ⁡ α = 5 13

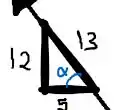
Então

M x = - 520 ⋅ 5 13 ⋅ 4 ⋅ cos ⁡ 30 ° = - 692,82   N

M y = 520 ⋅ sin ⁡ α ⋅ ( 6 + 4 ⋅ sin ⁡ 30 ° )

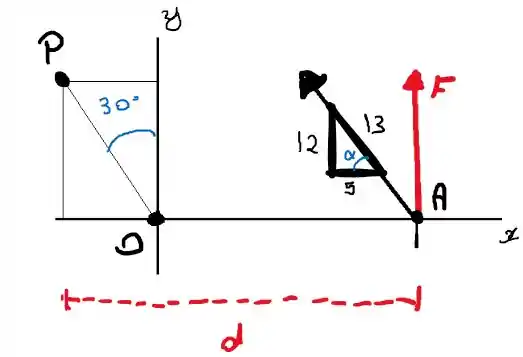
Novamente pelo triângulo temos

sin ⁡ α = 12 13

Então

M y = 520 ⋅ 12 13 ⋅ ( 6 + 4 ⋅ sin ⁡ 30 ° ) = 3840   N

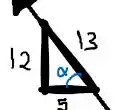
Então ficamos com

M = - 692,82 + 3840 = 3147,18   N ⋅ m = 3,147     k N ⋅ m

Resposta

M = 3,147   k N ⋅ m

Seu sentido é anti-horário.

Ver Outros Exercícios desse livro