Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 1.Problemas - Ex. 16
1.16. Usando as unidades básicas do SI, mostre que a Equação 1.2 é uma equação dimensionalmente homogênea que resulta F em newtons. Determine com três algarismos significativos a força gravitacional agindo entre duas esferas que estão se tocando. A massa de cada esfera é 200 kg e o raio é 300 mm.
Passo 1
A equação 1.2 é a seguinte
Onde é a massa e está em (quilogramas),
é a distância e está em (metros),
é a constante gravitacional, e sua unidade é
E é a força em (newtons), que é
Uma equação dimensionalmente homogênea é uma equação onde ambos os lados tem a mesma unidade dimensional.
Passo 2
Vamos fazer a análise dimensional agora
Assim provamos que a equação é dimensionalmente homogênea.
Passo 3
Agora vamos determinar a força gravitacional que o exercício pede.
Esse é um esboço da situação
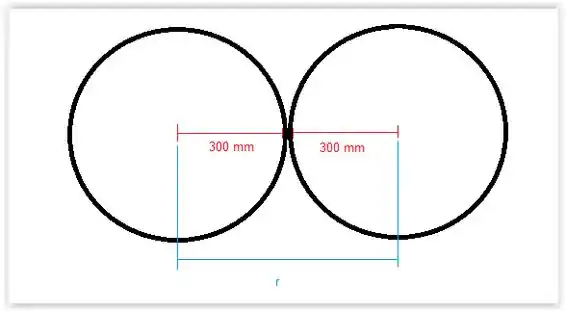
Passo 4
Já temos todos os elementos, agora basta calcular