Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 60

11.60 Cargas axiais de intensidade P são aplicadas paralelamente ao eixo geométrico da coluna A B e interceptam o eixo x , a uma distância e = 12   m m do eixo geométrico. Para o tipo de aço usado σ e = 250   M P a e E = 200   G P a . Sabendo-se que um coeficiente de segurança, em relação a deformação permanente, de 2,5 é desejado, determinar: (a) a intensidade P da carga admissível quando o comprimento L é 4,25   m ; (b) a relação entre a carga encontrada na parte a e a intensidade da carga centrada admissível para a coluna.

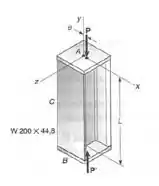
Passo 1

E ai gurizada tudo certo? O enunciado pede que a gente determine: (a) a intensidade P da carga admissível quando o comprimento L é 4,25   m ; (b) a relação entre a carga encontrada na parte a e a intensidade da carga centrada admissível para a coluna.

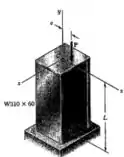
Vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

W 200 × 44,8

A = 5700   m m 2

I x = 70,8 × 10 6   m m 4

I z = 6,95 × 10 6   m m 4

r z = 34,8   m m

w z = 93,9 × 10 3   m m 3

L e = L = 4250   m m

Passo 2

Vamos começar determinando a força P pedida no item (a), partiu?

L r = 4250   m m 34,8   m m = 122,12

w = I c

c = I w = 6,95 × 10 6   m m 4 93,9 × 10 3   m m 3 = 74,01   m m

e * c r 2 = 12 * 74,01 34,8 2 = 0,733

Passo 3

Agora buscando no ábaco do livro para P A ≅ 80   M P a :

P C R 5700 = 80

P C R = 456000   N = 456   k N

Utilizando o fator de segurança dado e a relação abaixo podemos determinar o valor da força P .

P C R = P * F S

P = 456   k N 2,5

P = 182,4   k N

Passo 4

Show de bola! No item (b) precisamos determinar a relação entre a carga encontrada na parte a e a intensidade da carga centrada admissível para a coluna. Para isso, temos que:

P C R = π 2 E I L e 2 = π 2 200 × 10 3 6,95 × 10 6 4250 2

P C R = 759515,57   N = 759,52   k N

Novamente, como P C R = P * F S :

P = P C R F S

P = 759,52   k N 2,5

P = 303,81   k N

Passo 5

Comparando os resultados obtidos da força P nos itens (a) e (b):

P a P b = 182,4   k N 303,81   k N

P a P b = 0,6

Resposta

(a)

P = 182,4   k N

(b)

P a P b = 0,6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de com a a seção transversal mostrada e é usado como uma coluna, sabendo-se que σ e =320MPa e E=200GPa, determinar a carga centrada admissível, se o comprimento efetivo da coluna é de:(a) 9,6m
Uma coluna com a seção transversal mostrada tem um comprimento efetivo de 4,0m. Sabendo se que σ e = 250Mpa e E=200GPa, determinar a maior carga centrada que pode ser aplicada a coluna.
Uma carga axial P é aplicada em um ponto localizado sobre o eixo x, a uma distância e=15,2mm do eixo geométrico do perfil laminado de aço W200x41,7 da coluna BC. Sabendo-se que a coluna está livre em
Um tubo estrutural retangular tem a seção transversal mostrada e é usado como uma colunade 5m de comprimento efetivo. Sabendo-se que σ c = 250Mpa e E=200GPa, determinara maior carga centrada que pode
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usadoE=12GPa e que a