Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 12

12- - Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo y .

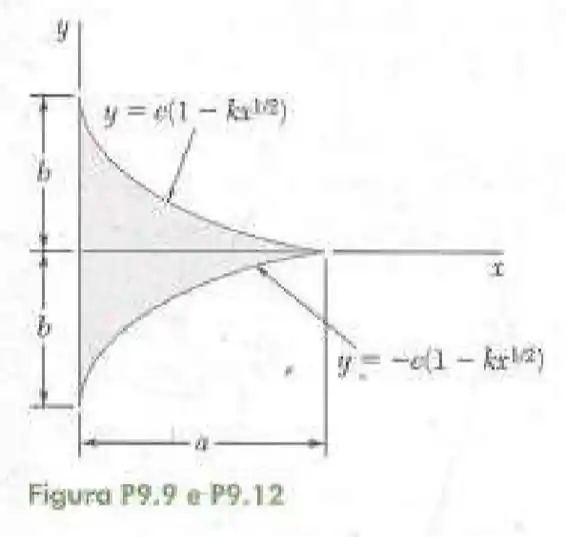
Passo 1

Se aplicarmos o ponto do gráfico superior igual a ( 0 , b ) nós encontramos uma constante igual a:

b = c 1 - 0 → c = b

E se aplicarmos o ponto ( a , 0 ) :

0 = b 1 - k a 1 2

k = 1 a 1 2

Dessa forma se aplicarmos linhas verticais para encontrar o elemento de área desse gráfico nós teremos:

d A = 2 b 1 - x a 1 2

Como todas as listras verticais tem valores iguais de y então não é necessário nenhuma correção.

Passo 2

Dessa forma nossa integral fica:

I y = ∫ x 2   d A

Com x variando de 0 até a

I y = ∫ 0 a x 2   2 b 1 - x a 1 2   d x

I y = 2 b ∫ 0 a x 2 - x 5 2 a d x

I y = 2 b x 3 3 - 2 x 7 2 7 a 0 a

I y = 2 b a 3 3 - 2 a 3 7

I y = 2 b a 3 21

I y = 2 a 3 b 21

Resposta

I y = 2 a 3 b 21

Ver Outros Exercícios desse livro