Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 18

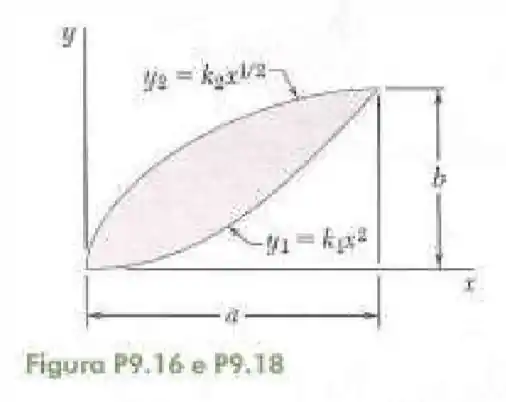
18- Determine o momento de inércia e o raio de giração da superfície sombreada mostrada na figura em relação ao eixo y .

Passo 1

Dessa vez queremos a inércia em relação ao eixo y e por isso vamos utilizar eixos verticais para calcular o elemento de área que será dado da seguinte forma:

d A = k 2   x 1 2 - k 1 x 2 d x

Com

k 1 = b a 2 ; k 2 = b a 1 2

Visto na questão 16, além da área ser igual a:

A = a b 3

Passo 2

Dessa forma a integral será:

I y = ∫ x 2   d A

Com x variando de 0 até a :

I y = ∫ 0 a x 2 × k 2   x 1 2 - k 1 x 2 d x  

I y = ∫ 0 a k 2 x - k 1 x 4 d x

I y = b a 1 2   2 x 7 / 2 7 - b a 2 x 5 5 0 a    

I y = 2 a 3 b 7 - a 3 b 5 = 3 a 3 b 35

Passo 3

E o raio de giro dessa inércia será calculado por:

k = I y A

k = 3 a 3 b 35 a b 3 = 9 a 2 35 = 3 a 1 35

Resposta

I y = 3 a 3 b 35

k = 3 a 1 35

Ver Outros Exercícios desse livro