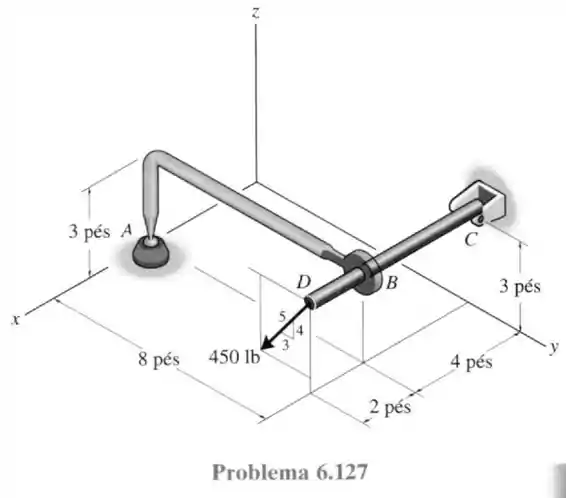
127- A estrutura mostrada na figura está submetida a uma força de que se orienta paralelamente ao plano . O elemento é sustentado por uma junta esférica em e se encaixa sem folga a um orifício em . O elemento é apoiado por um pino em . Determine os componentes e das reações em e .
Passo 1
A junta esférica em oferece reações nos três eixos a força e o pino em pode rotacionar em logo ele resiste a forças nos três eixos e a momentos em e . Além de que a força de de forma vetorizada fica da seguinte forma:
Analisando as forças e reações na barra .
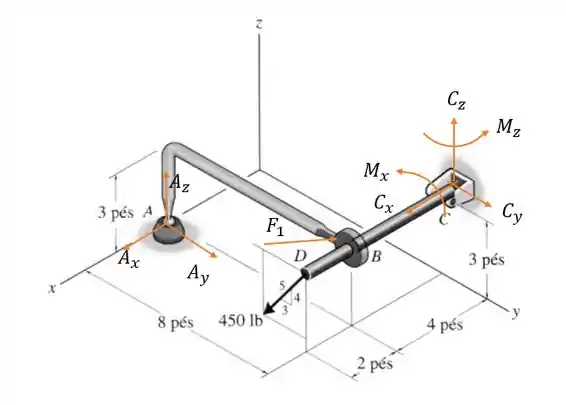
Onde é a força causada por toda a barra na barra que terá a seguinte angulação:
Logo a somatória das forças em nos dará:
A somatória das forças em nos dará:
Agora a somatória das forças em :
Passo 2
Agora para o somatório dos momentos:
Momentos em :
Momentos em :
Logo:
Agora os momentos em :
Passo 3
Agora vamos analisar as forças no elemento .
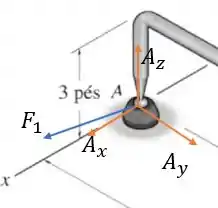
Onde deveremos inverter a força, assim como nas outras questões do tipo.
Fazendo a somatória das forças em nós teremos:
A somatória das forças em :
E a somatória das forças em :