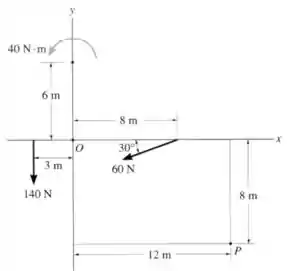
Substitua o sistema de forças e momentos por uma força e momento equivalentes ao sistema, atuantes no ponto .
Passo 1
O primeiro passo é calcular o momento resultante em relação ao ponto . Começamos analisando o momento da força de .
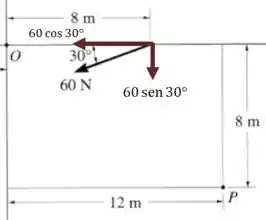
Só precisamos multiplicar cada componente da força pela sua distância perpendicular até a origem:
E vamos fazer o mesmo para a força de , que tem apenas um componente em :
Então o momento resultante em relação à origem é:
E o último termo se refere ao binário de que está representado no desenho:
Passo 2
Já temos o momento que deve ser aplicado em , mas falta ainda calcular a força. Temos que somar vetorialmente as duas forças que estão aplicadas no desenho:
Então a força resultante é:
Podemos definir essa força a partir de um módulo e um ângulo:
E para encontrar o ângulo formado com o semi-eixo negativo:
Resposta
As forças podem ser substituídas por um par formado por uma força de a do semieixo negativo no ponto , e um binário de .