Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 13

13- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo y .

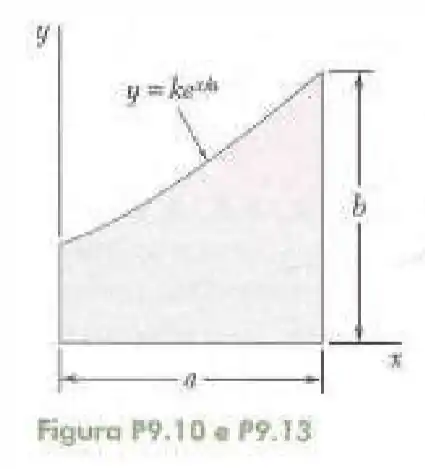
Passo 1

Supondo que vamos adquirir a área elementar por linhas verticais nós podemos dizer que:

d A = y   d x

E pela questão 10 nós conseguimos dizer que a equação vale:

y = b e   e x a

Passo 2

Dessa forma a inércia em y será:

I y = ∫ x 2   y   d x

I y = b e ∫ 0 a x 2   e x a   d x

Pois x varia de 0 até a .

Por integração por partes nós temos:

∫ u   d v = u v - ∫ v d u

u = x 2 → d u = 2 x

d v = e x a → v = a   e x a

Logo:

∫ x 2   e x a   d x = a x 2   e x a - ∫ 2 a x   e x a   d x

Agora:

∫ x   e x a   d x

u = x → d u = d x

d v = e x a → v = a   e x a

Dessa forma:

∫ x   e x a   d x = a x e x a - ∫ a e x a

Juntando tudo:

∫ x 2   e x a   d x = a x 2   e x a - 2 a a x e x a - a 2 e x a

= a x 2 e x a - 2 a 2 x e x a + 2 a 3 e x a

Cuidado com os sinais!

Aplicando o intervalo indo de 0 até a nós teremos:

I x = b e a 3 e - 2 a 3 e + 2 a 3 e - 2 a 3

I x = - 2 e b a 3 + b a 3 = 0.2642 a 3 b

Resposta

I x = 1 - 2 e b a 3

Ver Outros Exercícios desse livro