Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 17

17- Determine o momento de inércia e o raio de giração da superfície sombreada mostrada na figura em relação ao eixo y .

Passo 1

Como queremos agora a inércia em torno do eixo y vamos traçar linhas verticais para calcular o elemento de área dessa superfície:

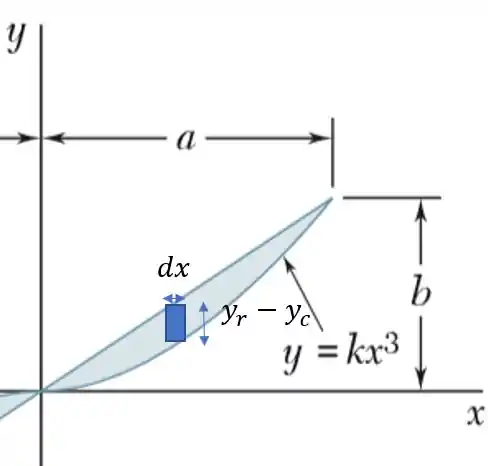
Onde y r é o y da reta e y c é o y da função cúbica.

Sabendo da questão passada que:

m = b a

k = b a 3

Logo:

d A = b x a - b x 3 a 3 d x

Passo 2

Com isso a inércia em y será calculada como:

I y = ∫ x 2   d A

Como x varia de - a até a nós podemos fazer o seguinte:

I x = ∫ - a a x 2   d A = 2   ∫ 0 a x 2   d A

I x = 2 ∫ 0 a x 2   b x a - b x 3 a 3 d x

I x = 2 ∫ 0 a b x 3 a - b x 5 a 3 d x

Fazendo a integral:

I x = 2 b x 4 4 a - b x 6 6 a 3 0 a

I x = 2 a 3 b 4 - a 3 b 6 = a 3 b 6

Passo 3

Podemos até pegar a área que calculamos na questão 15 mas vamos fazer a integral do d A que encontramos nessa questão para verificarmos um negócio rapidinho?

d A = b x a - b x 3 a 3 d x

Integrando em x de - a até a nós temos:

A = 2 ∫ 0 a b x a - b x 3 a 3 d x

A = 2 b x 2 2 a - b x 4 4 a 3 0 a

Aplicando o intervalo:

A = 2 b a 2 - a b 4 = a b 2

Mesma coisa!

Dessa forma o raio de giro será:

k = I y A

Aplicando os valores temos:

k = a 3 b 6 a b 2 = a 2 3 = a 3

Resposta

I x = a 3 b 6

k = a 3

Ver Outros Exercícios desse livro