Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 9

9- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo x .

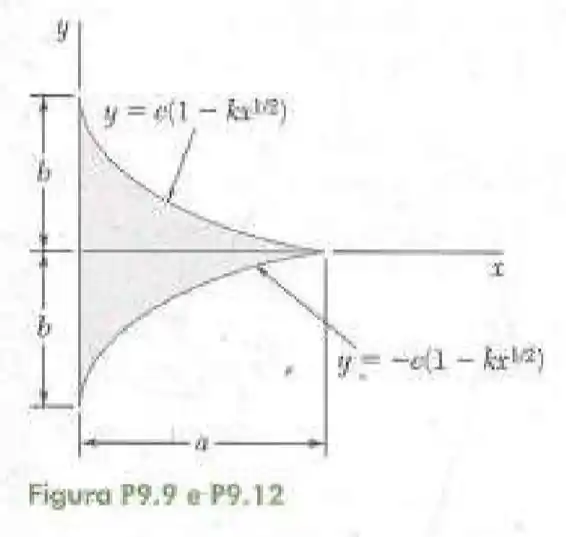
Passo 1

A integral para calcular a inércia no eixo x será:

I x = ∫ y 2   d A

E se fizermos o elemento de área por linhas verticais nós teremos:

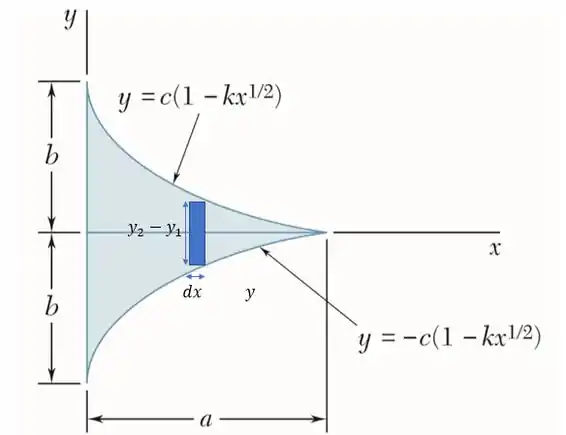
Dessa forma d A será:

d A = c 1 - k x 1 2 - - c 1 - k x 1 2 d x

d A = 2 c 1 - k x 1 2 d x

Onde k no ponto ( a , 0 ) vale:

0 = c 1 - k a 1 2

k = 1 a 1 2

E c   no ponto ( 0 , b ) vale:

b = c 1 - 0 → c = b

Logo temos a curva:

y = b 1 - x 1 2 a 1 2

Passo 2

Como essa região é simétrica em y podemos considerar somente a parte de cima do gráfico.

Sabendo que x varia de 0 até a da seguinte forma e como todos os elementos verticais tem posições de x diferentes entre si então devemos colocar o fator de 1 / 3 de correção:

I x = 1 3 ∫ 0 a y 2 ×   2 b 1 - x 1 2 a 1 2 d x

I x = 2 3 ∫ 0 a b 3   1 - x 1 2 a 1 2 3   d x

I x = 2 b 3 3 ∫ 0 a 1 - 3 x a 1 2 + 3 x a - x a 3 2   d x

I x = 2 b 3 3 a + 3 a 5 - 3 a 2

I x = 2 a b 3 3 0

I x = a b 3 15

Resposta

I x = a b 3 15

Ver Outros Exercícios desse livro