Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.Revisão - Ex. 130
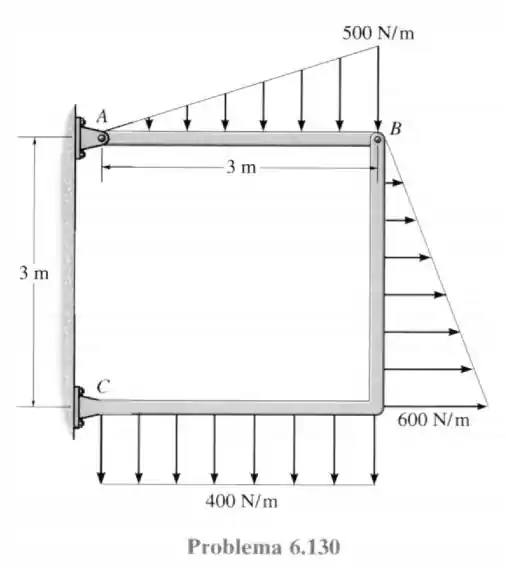
130- Determine os componentes horizontais e verticais das forças nos pinos e da estrutura de dois elementos.
Passo 1
Como a estrutura tem dois elementos vamos separar os dois corpos e traçar as forças resultantes geradas pelas cargas.
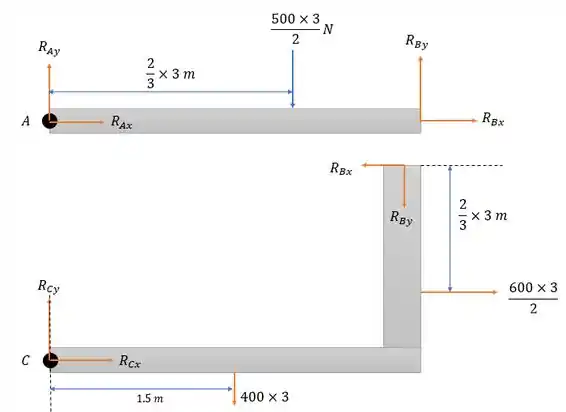
Onde traçamos todas as forças resultantes geradas pelas cargas e as distâncias aos pontos.
Passo 2
Vamos começar pela barra calculando inicialmente a força vertical :
Calculando os momentos em .
Com essa força vamos calcular a reação vertical em pela somatória das forças verticais nessa barra.
Passo 3
Agora vamos calcular a reação horizontal em ao fazer a somatória dos momentos em na barra de baixo.
Onde adotamos o sentido horário como positivo.
Fazendo então a somatória das forças horizontais na barra ser zero teremos:
Passo 4
Agora podemos calcular as reações no ponto fazendo a somatória das forças na barra de baixo.
Fazendo a somatória das componentes verticais temos:
Fazendo a somatória das forças horizontais temos a outra componente da força em :