34- Determine a força nos elementos e da treliça, que é utilizada como apoio do piso de uma ponte. Indique se esses elementos estão sob tração ou compressão.
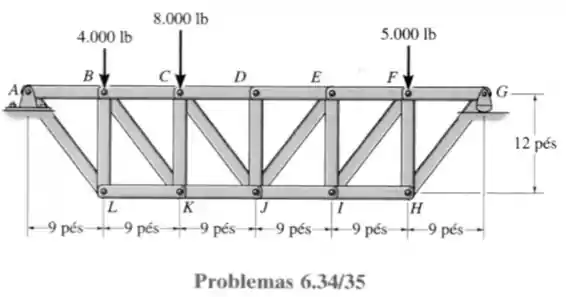
Passo 1
Sabendo que não há reações horizontais na estrutura acima vamos calcular as reações verticais nos apoios e .
A viga equivalente seria tal que:
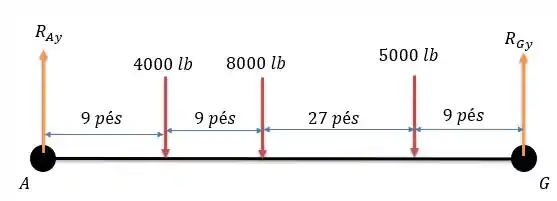
Calculando a somatória da forças verticais nós temos:
Calculando a somatória dos momentos em será:
Isso nos dá:
Passo 2
Primeiramente vamos cortar as barras e e vamos analisar a estrutura a direita desse corte para encontrar essa três forças.
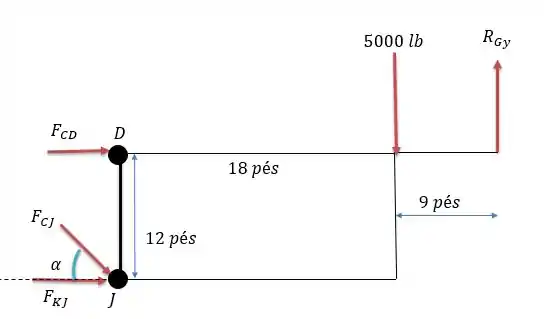
Onde valerá:
Como todas as forças estão entrando no nó logo o sinal positivo seria uma força compressiva.
Fazendo a somatória das forças verticais nós teremos:
Logo será:
Como a força está entrando no nó então essa força é uma força de compressão.
Passo 3
Agora vamos calcular os momentos em
Por considerarmos a força entrando no nó o sinal negativo nos mostra que essa força é uma força trativa.
E o somatório dos momentos em :
O que se configura em uma força compressiva.
Passo 4
Por uma simples análise no nó temos:
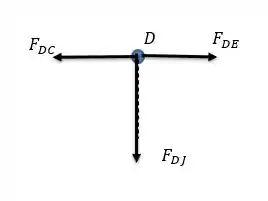
Se fizermos a somatória das forças verticais nós teremos: