14- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Considere que , e .
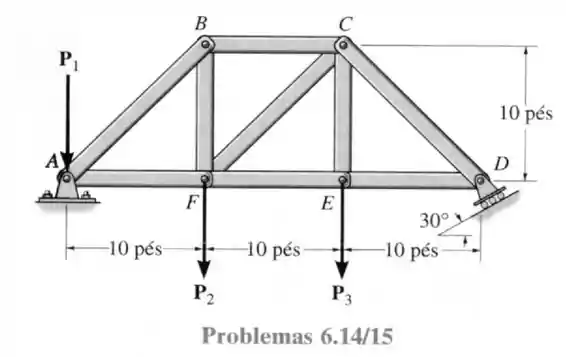
Passo 1
Vamos desenhar a estrutura equivalente para calcular as reações do sistema.
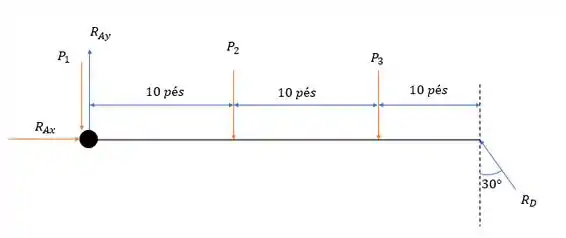
Onde e valem respectivamente e . Logo pela somatória das forças verticais teremos:
Agora fazendo a somatória dos momentos em temos:
Logo:
Agora fazendo a somatória das forças horizontai nós vamos ter:
Passo 2
Agora vamos nó por nó encontrar as forças nas barras, vamos começar pelo nó .
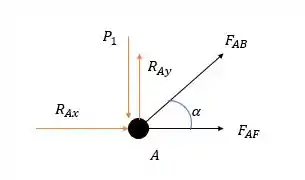
Onde vale:
Fazendo a somatória das forças verticais temos:
Força compressiva.
Agora a força horizontal nos dará:
Força trativa.
Passo 3
Agora vamos analisar as forças no nó :
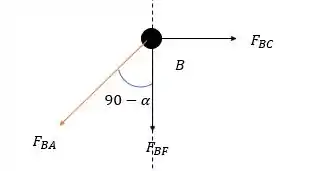
Fazendo a somatória das forças verticais temos:
Força trativa.
Agora a somatória das forças horizontais:
Passo 4
Agora vamos para as forças em :
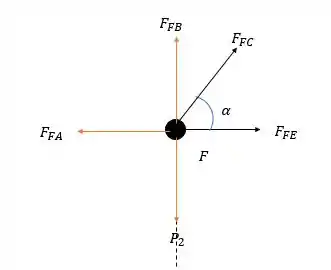
Fazendo a somatória das forças verticais temos:
Agora fazendo a somatória das forças horizontais:
Passo 5
Agora para o nó :
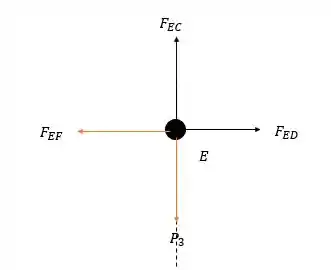
Essa é bem simples pela soma das forças verticais e horizontais:
Isso abre a possibilidade de podermos calcular as forças no nó (que só falta uma).
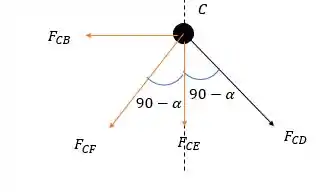
Fazendo a somatória das forças verticais temos: