25- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Dica: o componente vertical da força em deve ser igual a zero. Por quê?
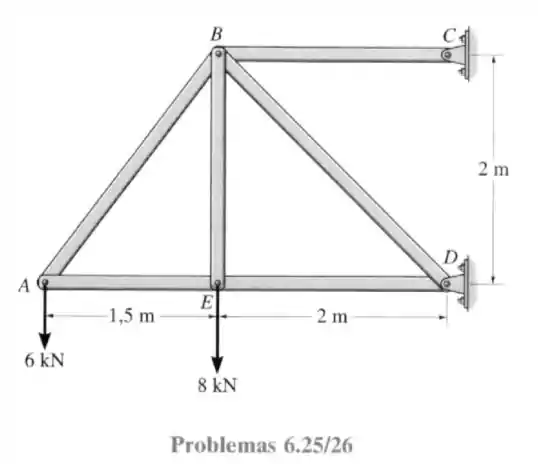
Passo 1
O apoio em consegue resistir na horizontal e na vertical, porém nesse ponto só teremos uma força de ação no sentido de que está na horizontal então fazendo a somatória das forças verticais no ponto nós teremos um fazendo com que toda a força vertical seja resistida em .
Isso nos dá o seguinte diagrama de forças.
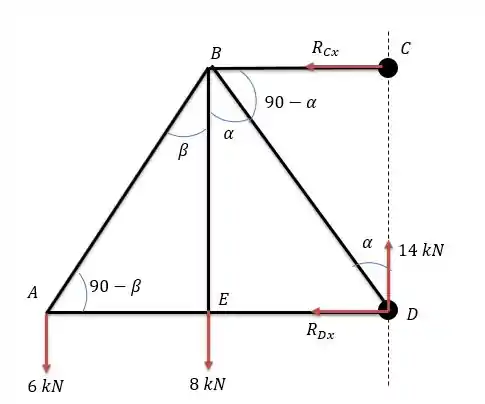
Onde vale:
E o valor de :
Fazendo a somatória dos momentos em conseguimos encontrar as reações horizontais.
Logo pela somatória das forças horizontais vale:
O que nos dá uma força na barra igual a:
Passo 2
Vamos começar pelo nó .
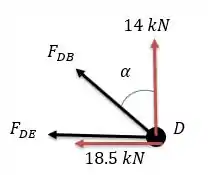
Fazendo a somatória das forças verticais temos:
O que faz ser uma força compressiva.
Agora fazendo a somatória das forças horizontais:
Força negativa, portanto compressiva.
Passo 3
Agora vamos analisar o nó .
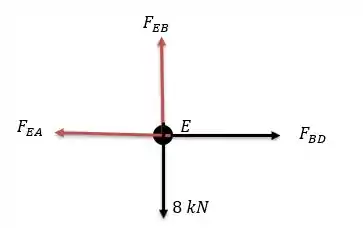
Pela somatória das forças verticais conseguimos:
E a somatória das forças horizontais:
Passo 4
Agora vamos resolver para o nó que já nos dará as forças de todas as treliças.
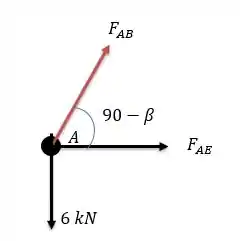
Fazendo a somatória das forças verticais nós teremos:
Onde vale logo valerá:
Força trativa.