Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 14

14- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo y .

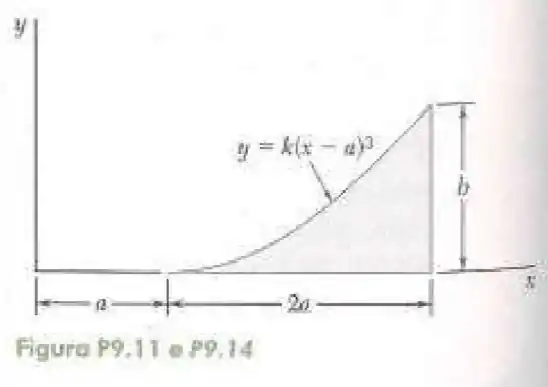
Passo 1

Ainda na idéia de utilizar linhas verticais para verificar o elemento de área d A nós temos da questão 11:

d A = y   d x

Onde:

y = b 8 a 3   x - a 3

Passo 2

O que nos dá um momento de inércia em y igual a:

I y = ∫ x 2   d A

I y = b 8 a 3 ∫ x 2   y   d x

Como x varia de a até 3 a nós teremos:

I y = b 8 a 3 ∫ a 3 a x 2   x - a 3   d x

Abrindo esse polinômio nós temos:

I y = b 8 a 3 ∫ a 3 a x 2 x 3 - 3 a x 2 + 3 a 2 x - a 3 d x

I y = b 8 a 3 ∫ a 3 a ( x 5 - 3 a x 4 + 3 a 2 x 3 - a 3 x 2 ) d x

Fazendo a integral:

I y = b 8 a 3 x 6 6 - 3 a x 5 5 + 3 a 2 x 4 4 - a 3 x 3 3 a 3 a

Isso nos dá:

I y = b 8 a 3 3 a 6 6 - 3 a 3 a 5 5 + 3 a 2 3 a 4 4 - a 3 3 a 3 3 - a 6 6 - 3 a × a 5 5 + 3 a 2 a 4 4 - a 3 a 3 3

I y = b 8 a 3 729 a 6 6 - 729 a 6 5 + 243 a 6 4 - 27 a 6 3 - a 6 6 - 3 5 a 6 + 3 4 a 6 - a 3 3

I y = a 3 b 8 412 15 = 103 a 3 b 30

Resposta

I y = 103 a 3 b 30

Ver Outros Exercícios desse livro