Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 16

16- Determine o momento de inércia e o raio de giração da superfície sombreada mostrada na figura em relação ao eixo x .

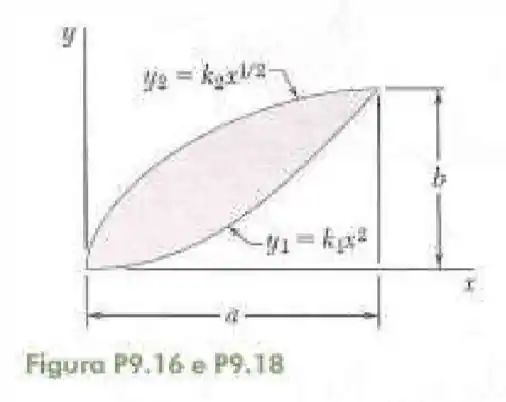
Passo 1

Aplicando o ponto ( a , b ) nós conseguimos encontrar os valores de k nas duas equações:

b = k 2 a 1 2 → k 2 = b a 1 2

b = k 1 a 2 → k 1 = b a 2

E se fizermos por linhas horizontais nós encontramos:

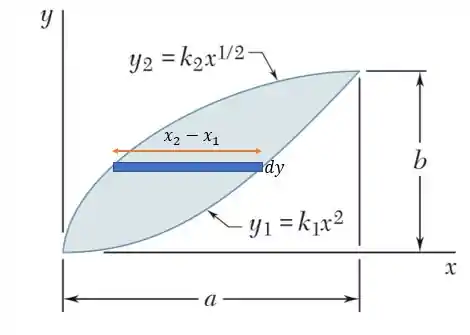
Onde:

x 1 = y k 1

x 2 = y 2 k 2 2

Passo 2

Logo a integral em relação a x , com y variando de 0 até b , valerá:

I x = ∫ 0 b y 2 y k 1 - y 2 k 2 2 d y    

Como x é igual a todos os elementos que estamos pegando logo não há o acerto de 1 / 3 .

I x = ∫ 0 b y 5 k 1 - y 4 k 2 2 d y

I x = 2 y 7 2 7 k 1 - v 0 b

I x = 2 b 7 2 7 k 1 - b 5 5 k 2 2

Substituindo os valores de k 1 e k 2 temos:

I x = 2 a b 7 2 7   b 1 2 - a b 5 5 b 2 = 2 a b 3 7 - a b 3 5

I x = 3 a b 3 35

Passo 3

Para encontrar o raio de giro precisamos aplicar a fórmula:

k = I x A

Onde I x já encontramos do passo anterior, falta agora a área e para isso vamos aplicar a fórmula:

A = ∫ y   d x

Onde y é a linha que vai de y 2 até y 1 . Note que poderia ser A = ∫ x   d y com x sendo a mesma linha indo de x 1 até x 2 . A escolha é sua e de qualquer jeito tem que dar o mesmo resultado.

A = ∫ 0 a k 2 x 1 2 - k 1 x 2 d x

A = 2 3 k 2   x 3 2 - k 1 x 3 3 0 a = 2 b 3 a 1 2 a 3 2 - b 3 a 2 a 3 = 2 b a 3 - b a 3 = b a 3

Logo o raio de giro vale:

k = 3 a b 3 35 a b 3 = 9 b 2 35 = 3 b 1 35

Resposta

I x = 3 a b 3 35

k = 3 b 1 35

Ver Outros Exercícios desse livro