141. O barco deve ser puxado para a praia usando-se duas cordas. A força resultante é de , orientada ao longo do casco, dado pela linha , como mostrado na figura. Determine as intensidades das forças e que atuam em cada corda e o ângulo , de modo que seja mínima. atua a da quilha, como mostra a figura.
Passo 1
Para resolver esse problema temos, que lembrar que e são vetores e a soma deles da um vetor que é horizontal, então se organizarmos eles de forma a entender melhor essa soma, vamos ter o seguinte:
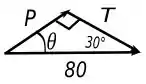
Visto essa relação, vemos que é formado um triângulo e já aprendemos que a soma dos ângulos internos de um triângulo é
Logo:
Que é a condição de que seja mínimo.
Para achar e , vamos usar a lei dos senos ao nosso favor, que diz o seguinte:
Dado um triângulo qualquer:
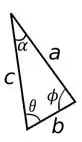
Temos que:
Passo 2
Agora vamos usar a lei dos senos para achar , temos:
Passo 3
Agora vamos usar a lei dos senos para achar , temos: