Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 24

24- a ) Mostre que o raio de giração polar k O da superfície anelar mostrada na figura é aproximadamente igual ao raio médio R m = R 1 + R 2 2 para pequenos valores de espessura t = R 2 - R 1 b ) Determine o erro percentual cometido ao se usar R m no lugar de k O para os seguintes valores de t / R m : 1 , 1 2 e 1 10 .

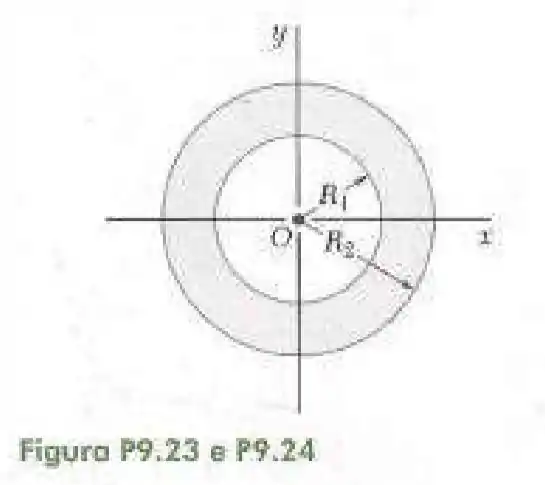
Passo 1

A área total dessa superfície será igual a:

A = π R 2 2 - π R 1 2 = π R 2 2 - R 1 2

E como a inércia polar descoberta na questão anterior vale:

J = π 2 R 2 4 - R 1 4

Logo:

k = J A = π 2 R 2 4 - R 1 4 π R 2 2 - R 1 2 = R 2 4 - R 1 4 2 R 2 2 - R 1 2

Isso é a mesma coisa que:

k = R 2 2 + R 1 2 R 2 2 - R 1 2 2 R 2 2 - R 1 2

k = R 2 2 + R 1 2 2

Passo 2

Agora vamos para o que significado do raio médio:

R m = R 1 + R 2 2

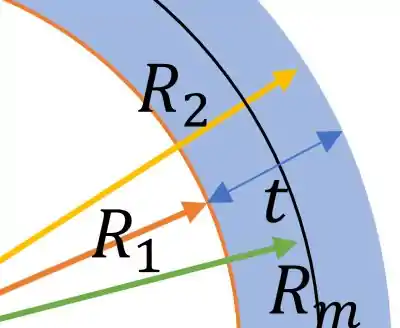
Ou seja:

R m = R 2 - t 2 = R 1 + t 2

R 1 = R m - t 2

R 2 = R m + t 2

Substituindo esses valores para o que encontramos de k nós temos:

k = R m + t 2 2 + R m - t 2 2 2

k = R m 2 + R m t + t 2 4 + R m 2 - R m t + t 2 4 2

k = 2 R m 2 + t 2 2 2

Fazendo limite de t tender a zero nós temos:

k = R m

Passo 3

Para t = R m teremos:

k = 2 R m 2 + R m 2 2 2 = 5 R m 2 4 = R m 5 4

Como o erro é calculado por:

e r r o = v a l o r   a p r o x i m a d o - v a l o r   r e a l v a l o r   r e a l × 100

Nós temos:

e r r o = R m - 5 4 R m 5 4 R m × 100 = - 10.56 %

Passo 4

Agora para t = R m 2 temos:

k = 2 R m 2 + R m 2 8 2 = 17 R m 2 16 = 17 4 R m

Logo o valor do erro será:

e r r o = R m - 17 4 R m 17 4 R m × 100 = - 2.99 %

Passo 5

Agora para t = R m 10 :

k = 2 R m 2 + R m 2 2 × 100 2 = 2 R m 2 + R m 2 200 2 = 401 R m 2 400

Dessa formo o erro será:

e r r o = R m - 401 R m 2 400 401 R m 2 400 × 100 = - 0.125 %

Resposta

a )   P a s s o s   1   e   2

b ) - 10.56 % ; -   2.99 % ; - 0.125 %  

Ver Outros Exercícios desse livro