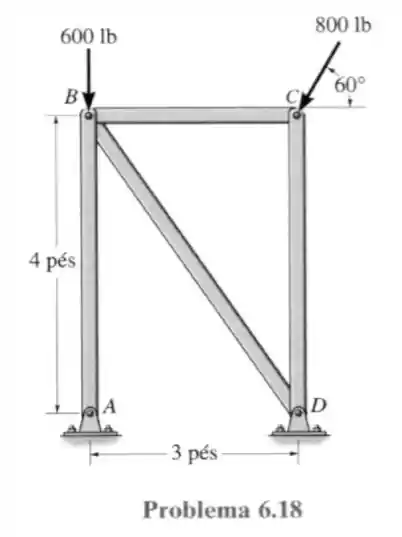
18- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Dica: o componente horizontal da força em deve ser nulo. Por quê?
Passo 1
Fala projetista de prédio de três andares, vamos resolver mais essa questão aqui.
Se fizermos a somatória das forças horizontais em nós encontraremos que a componente em será zero, pois a única força presente nela são forças verticais (a reação com o chão e com a barra ). Logo toda a componente horizontal resistente estará em .
Porém não precisamos calcular essas reações já que a estrutura é bem simples, vamos apenas nos preocupar com as juntas e só com elas conseguimos encontrar as forças em todas as barras.
Para o nó .
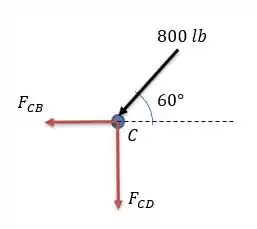
Considerando que e são forças resistentes as forças externas, então se elas forem positivas teremos uma tração nas barras.
Fazendo a somatória das forças horizontais temos:
O que é uma força compressiva, uma vez que consideramos essa força uma força saindo do nó (então essa força é uma força que se opõe a compressão da barra).
Agora fazendo a somatória das forças verticais temos:
O que é uma força compressiva.
Passo 2
Agora vamos para o nó .
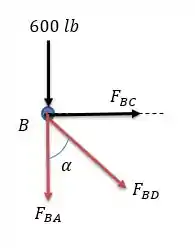
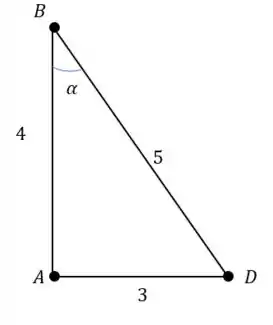
Onde é um ângulo que está dentro de um triângulo 3,4,5 cujo cosseno vale e o seno vale . Fazendo a somatória das forças horizontais temos:
Força trativa.
Para achar a força faltante vamos fazer a somatória das forças verticais:
Força compressiva.
Resposta
Se fizermos a somatória das forças horizontais em nós encontraremos que a componente em será zero. Logo toda a componente horizontal resistente estará em .