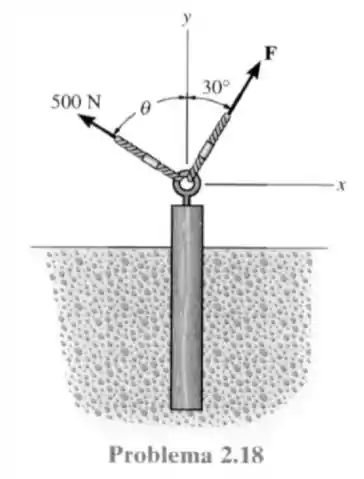
18- Duas forças são aplicadas na extremidade de um olhal a fim de remover a estaca. Determine o ângulo e a intensidade da força , de modo que a força resultante que atua sobre a estaca seja orientada verticalmente para cima e tenha intensidade de .
Passo 1
Fala meus futuros da nação! Vamos resolver mais uma questão desse livro maravilhoso. E para isso vamos começar desenhando os vetores das forças aplicadas nesse olhal
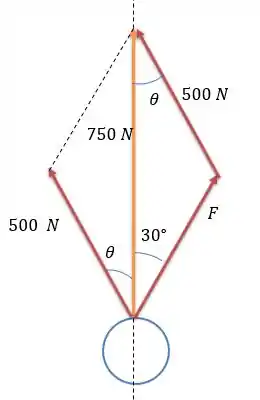
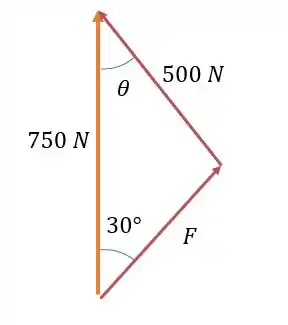
E tomamos aqui a liberdade de usar um paralelogramo de forças para projetar a força de em um triângulo de forças com a força resultante de que é dita no enunciado que é uma força orientada para cima.
Passo 2
Aplicando a lei dos cossenos nesse triângulo de forças conseguimos encontrar o valor de utilizando o ângulo de .
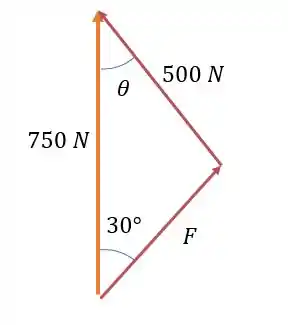
Lembrando que a lei dos cossenos é parecida com a lei de Pitágoras só que subtraindo de . Nessa fórmula, o nosso lado é o lado oposto ao ângulo, os lados e são os lados que acompanham o ângulo e vai ser o nosso ângulo, que aqui será o ângulo de . Ficamos então com:
Isso nos dá uma equação do segundo grau igual a:
Por Bhaskara encontramos raízes iguais a:
Porém não podemos encontrar um valor maior que (pois essa é a força resultante né, que é a soma entre a força e a força de , ou seja, tanto quanto a força precisam ser menores que ). Logo:
Passo 3
Perfeito galera! Já temos o valor de , então encontrar o valor do ângulo fica mole!
O valor de pode ser encontrado pela lei dos senos, você lembra da lei dos senos?
A lei dos senos diz para a gente que:
Onde esses senos embaixo dos lados são sempre referentes ao ângulo oposto ao lado. No nosso exemplo vai ficar mais claro!
Vamos voltar com nosso triângulo
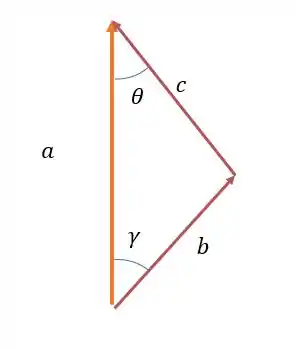
Com os ângulos que temos a lei dos senos pode ser vista como:
Então vendo pro triângulo do nosso problema nós temos:
E a lei dos senos fica:
Isolando e aplicando o que encontramos no passo anterior temos:
Fazendo o arco seno nesse ângulo nós acharemos o ângulo em graus igual a: