22- Determine a intensidade e a direção da resultante das três forças, encontrando primeiro a resultante e depois compondo .
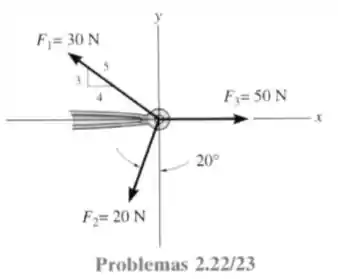
Passo 1
Essa questão eu faço por lei dos cossenos pois na próxima seção terá uma questão para se fazer por decomposição.
Desenhando o triângulo de forças para e temos:
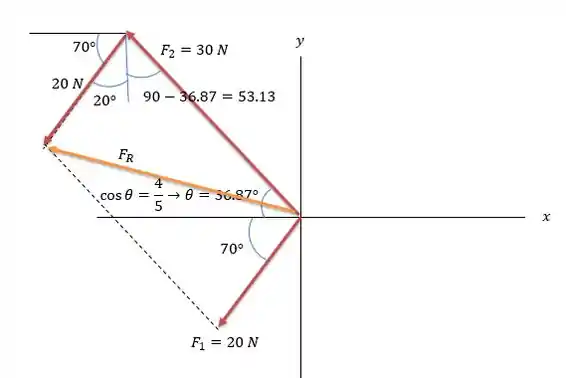
Pela lei dos cossenos temos:
Passo 2
Porém para poder avançar é importante saber que ângulo ela faz com o eixo , pois é nesse eixo onde se encontra a próxima força, para isso vamos utilizar a próxima figura.
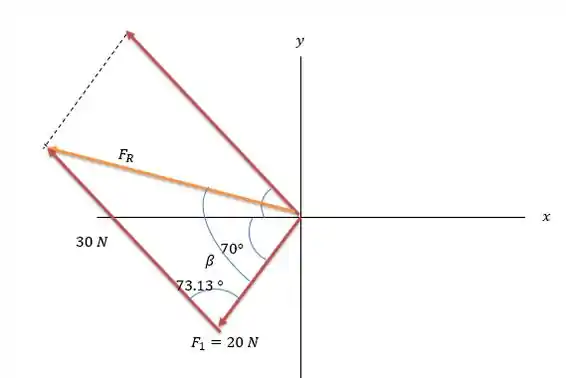
Pela lei dos senos:
Isso significa que a força está abaixo do eixo .
Passo 3
Redesenhando a força e colocando agora a força temos:
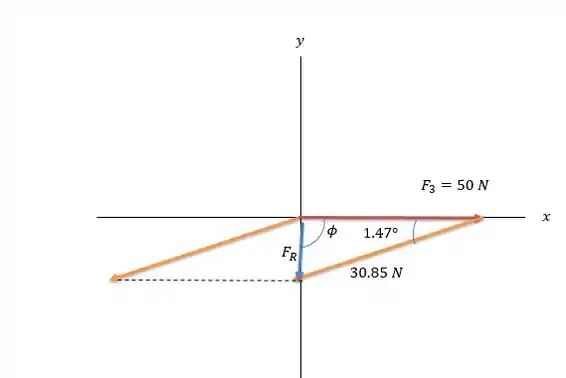
Pela lei dos cossenos temos
E está em um ângulo em relação ao eixo igual a:
Não tenha vergonha de desenhar errado as forças!