Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.3 - Ex. 2

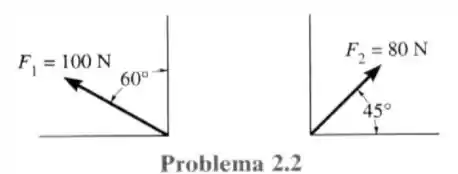
2- Determine a intensidade da força resultante se:

  1. F r = F 1 + F 2
  2. F r ' = F 1 - F 2

Passo 1

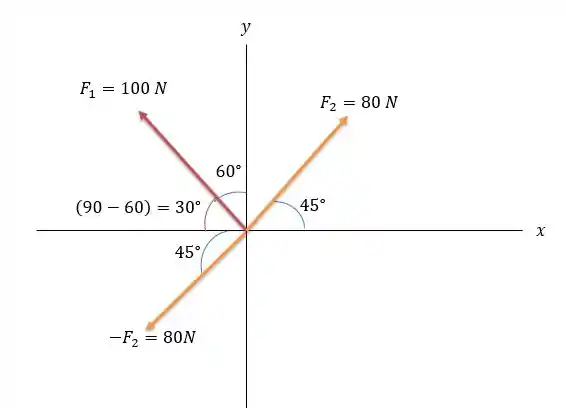
Vamos fazer a letra a decompondo os vetores e a letra b fazendo pela lei dos cossenos (já que ela precisará redesenhar um vetor). Dessa forma a letra a ficará com os seguintes vetores decompostos.

F 1 = ( - 100 sin ⁡ 60 ) i ^ + ( 100 cos ⁡ 60 ) j ^ = - 86.60 i ^ + 50 j ^

F 2 = ( 80 cos ⁡ 45 ) i ^ + ( 80 sin ⁡ 45 ) j ^ = 56.57 i ^ + 56.57 j ^

Passo 2

Logo se somarmos esses vetores decompostos teremos:

F r = F 1 + F 2 = - 86.6 + 56.57 i ^ + 50 + 56.57 j ^

F r → = - 30.03 i ^ + 106.57 j ^

Fazendo o módulo dessa força temos:

F = - 30.03 2 + 106.57 2 = 110.72   N

Passo 3

Como o vetor resultante F r ' deverá ser feita calculando F 1 - F 2 logo deveremos inverter o vetor F 2 . A figura mostra bem como isso é feito:

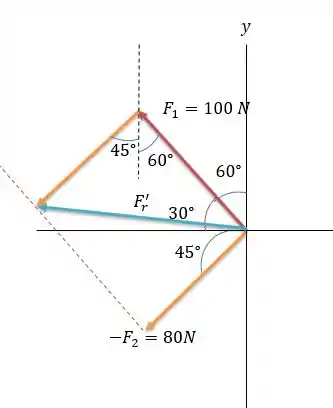
F 1 e - F 2 vamos utilizar a lei dos cossenos onde o ângulo entre formado entre eles é de:

θ = 45 + 60 = 10 5 °

Logo:

F r ' 2 = 100 2 + 80 2 - 2 × 100 × 80 cos ⁡ ( 10 5 )

F r ' = 20541.104 = 143.32   N

Esse é outro motivo para prefirir fazer por decomposição de vetor, a chance de errar ângulo (como nesse caso é bastante grande).

Resposta

a )   110.72   N

b )   143.32   N

Ver Outros Exercícios desse livro