Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.3 - Ex. 19

19- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão. Dica: a força resultante no pino E atua ao longo do elemento E D . Por quê?

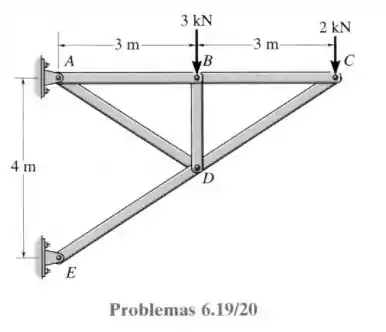
Passo 1

Vamos analisar primeiramente o nó C .

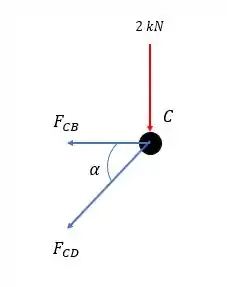
Onde α é calculada por:

α = tan - 1 ⁡ 4 6 = 33.69 °

Fazendo a somatória das forças verticais nós teremos:

2 + F C D sin ⁡ α = 0

F C D = - 2 sin ⁡ 33.69 = - 3.61   k N

Força essa sendo compressiva. Já que consideramos a força saindo do nó e encontramos sinal negativo.

Já a somatória das forças horizontais:

F C B + F C D cos ⁡ α = 0

F C B = - F C D cos ⁡ α = - - 3.61 cos ⁡ 33.69 = 3   k N

Força trativa.

Passo 2

Agora vamos para o nó B .

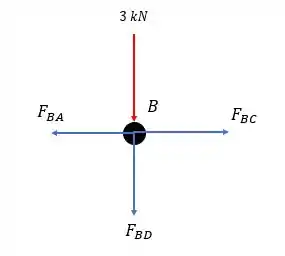
Fazendo a somatória das forças verticais:

F B D + 3 = 0

F B D = - 3   k N

Força esse sendo compressiva.

E a somatória das forças horizontais:

F B C = F B A = 3   k N   ( T )

Passo 3

Agora indo para o nó D , conseguimos encontrar as forças em todas as barras.

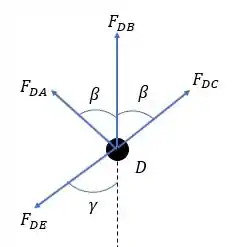
Onde os ângulos β e γ serão calculadas como:

γ = tan - 1 ⁡ 3 2 = 56.31 °

Uma vez que D está na metade da distância entre A e E e β pode ser calculado por:

β = 90 - α = 90 - 33.69 = 56.31 °

Logo, fazendo a somatória das forças verticais teremos:

F D B + F D C sin ⁡ β + F D A sin ⁡ β = F D E sin ⁡ γ

Isso dá:

- 3 - 3.61 cos ⁡ 56.31 + F DA cos ⁡ 56.31 = F D E cos ⁡ 56.31

F D E - F D A = - 3 - 3.61 cos ⁡ 56.31 cos ⁡ 56.31 = - 9.018336

Agora a somatória das forças horizontais:

F D C sin ⁡ 56.31 = F D A sin ⁡ 56.31 + F D E sin ⁡ 56.31

- 3.61 = F D A + F D E

Esse sistema nos dá:

F D E = 6.31   k N ( C )

Consequentemente:

F D A = 2.7   k N ( T )

Resposta

F C D = 3.61   k N   ( C )

F C B = 3   k N ( T )

F B D = 3   k N ( C )

F B A = 3   k N ( T )

F D E = 6.31   k N ( C )

F D A = 2.7   k N   ( T )

A junta E só tem uma barra conectada a ela, por isso as reações verticais e horizontais serão iguais a projeções da força da barra E D .

Ver Outros Exercícios desse livro